Python 中矩阵相乘的多种方法
本教程将深入探讨在 Python 中执行矩阵乘法的几种方法。 你将学习如何验证矩阵相乘的有效性,并通过编写自定义函数、使用列表推导式以及借助 NumPy 库来实现矩阵乘法。
首先,我们将回顾矩阵乘法成立的先决条件,随后探索如何使用 Python 构建自定义矩阵相乘函数。 之后,我们将探索使用嵌套列表推导式来实现相同目标的方法。 最后,我们将利用 NumPy 及其内置函数来执行高效的矩阵相乘操作。
矩阵乘法有效性检查
在深入研究 Python 代码之前,让我们首先回顾一下矩阵乘法的基本概念。
两个矩阵 A 和 B 之间的矩阵乘法运算,只有当矩阵 A 的列数与矩阵 B 的行数相等时,才是有效的。
你可能以前遇到过这样的条件,但你有没有思考过为什么会这样呢?
这与矩阵乘法的运算机制息息相关。请看下面的图示。
在我们的示例中,矩阵 A 的维度是 m 行 n 列,而矩阵 B 的维度是 n 行 p 列。
结果矩阵的维度
结果矩阵 C 中位于 (i, j) 索引位置的元素,是通过计算矩阵 A 的第 i 行与矩阵 B 的第 j 列的点积得到的。
因此,要获得结果矩阵 C 中特定索引位置的元素,需要分别计算矩阵 A 和 B 中对应行列的点积。
重复这个过程,最终会得到一个维度为 mxp 的结果矩阵 C,即 m 行 p 列,如下所示。
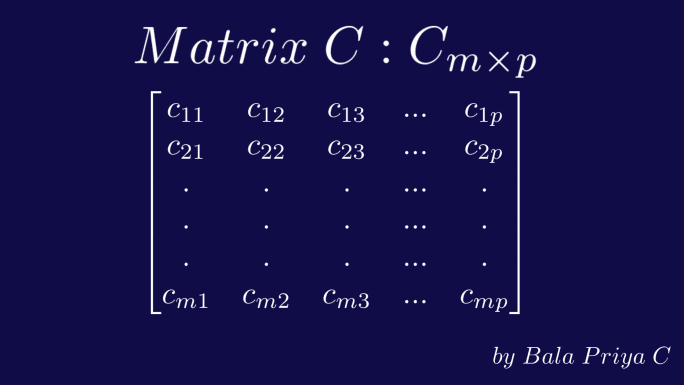
两个向量 a 和 b 的点积或内积,可以用以下公式表示。

总结一下:
- 显而易见的是,点积只在长度相等的向量之间定义。
- 因此,为了使行和列之间的点积运算有效(当两个矩阵相乘时),它们必须具有相同数量的元素。
- 在上面的例子中,矩阵 A 的每一行都有 n 个元素,而矩阵 B 的每一列也有 n 个元素。
仔细观察,你会发现 n 既是矩阵 A 的列数,也是矩阵 B 的行数。这解释了为什么矩阵 A 的列数必须等于矩阵 B 的行数。
希望现在你已经清楚地了解了矩阵乘法成立的条件,以及如何获得结果矩阵中的每一个元素。
接下来,让我们编写一些 Python 代码来执行矩阵乘法。
编写自定义的矩阵乘法 Python 函数
首先,让我们创建一个自定义函数来执行矩阵乘法。
这个函数应该:
- 接受两个矩阵 A 和 B 作为输入。
- 检查 A 和 B 之间的矩阵乘法是否有效。
- 如果有效,则将两个矩阵 A 和 B 相乘,并返回结果矩阵 C。
- 否则,返回一条错误信息,说明矩阵 A 和 B 不能相乘。
第一步:使用 NumPy 的 random.randint() 函数创建两个随机整数矩阵。你也可以将矩阵声明为嵌套的 Python 列表。
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"矩阵 A:\n {A}\n")
print(f"矩阵 B:\n {B}\n")
# 输出
矩阵 A:
[[4 9 9]
[9 1 6]
[9 2 3]]
矩阵 B:
[[2 2]
[5 7]
[4 4]]
第二步:定义函数 multiply_matrix(A, B)。该函数将两个矩阵 A 和 B 作为输入,如果矩阵乘法有效,则返回结果矩阵 C。
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(A.shape[0]):
for col in range(B.shape[1]):
for elt in range(A.shape[1]):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "对不起,矩阵 A 和 B 不能相乘。"
函数定义解析
让我们详细分析一下这个函数定义。
将 C 声明为全局变量:在 Python 中,函数内部定义的变量默认具有局部作用域,这意味着无法从函数外部访问它们。 为了使结果矩阵 C 能够从外部访问,我们将其声明为全局变量,只需在变量名前面加上 “global” 关键字。
检查矩阵乘法是否有效:使用 shape 属性来检查矩阵 A 和 B 是否可以相乘。对于任何数组 arr,arr.shape[0] 和 arr.shape[1] 分别返回行数和列数。因此,条件 A.shape[1] == B.shape[0] 用于检查矩阵乘法是否有效。只有当此条件为 True 时,才会计算结果矩阵;否则,函数将返回错误消息。
使用嵌套循环计算值:为了计算结果矩阵的元素,我们必须遍历矩阵 A 的行,外部 for 循环负责此操作。内部的 for 循环帮助我们遍历矩阵 B 的列。最内层的 for 循环用于访问选定列中的每个元素。
▶️ 现在我们已经理解了矩阵乘法 Python 函数的工作原理,让我们用之前生成的矩阵 A 和 B 调用该函数。
multiply_matrix(A,B)
# 输出
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
由于矩阵 A 和 B 之间的矩阵乘法运算有效,因此函数 multiply_matrix() 返回了结果矩阵 C。
使用 Python 嵌套列表推导式进行矩阵乘法
上一节中,你编写了一个 Python 函数来执行矩阵乘法。现在,我们将看到如何使用嵌套列表推导式来达到相同的目的。
下面是矩阵乘法的嵌套列表推导式。
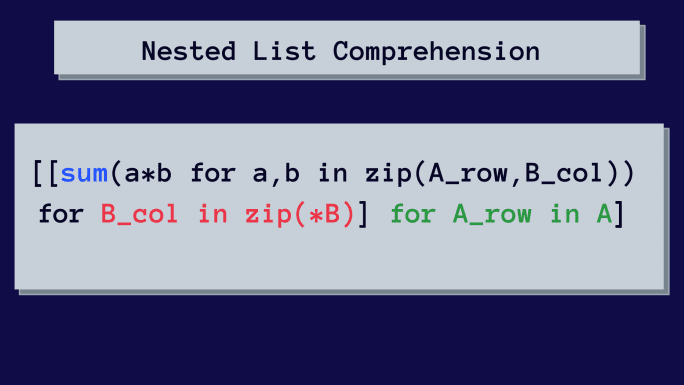
乍一看,这可能有点复杂,但我们会逐步分解这个嵌套列表推导式。
让我们一次只关注一个列表推导式,并确定它的作用。
我们将使用以下通用模板来表示列表推导式:
[<要做的操作> for <项目> in <可迭代对象>] 其中, <要做的操作>: 你想要执行的操作(表达式或运算) <项目>: 你想要对其执行操作的每个项目 <可迭代对象>: 你想要循环遍历的可迭代对象(列表、元组等)
▶️ 请参阅我们的 Python 列表推导式指南,以获得更深入的理解。
在继续之前,请注意,我们的目标是一次构建结果矩阵 C 的一行。
嵌套列表推导式详解
第一步:计算矩阵 C 中的单个值
给定矩阵 A 的第 i 行和矩阵 B 的第 j 列,以下表达式会给出矩阵 C 中索引位置 (i, j) 处的元素值。
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) 返回一个元组迭代器 # 如果 A_row = [a1, a2, a3] 和 B_col = [b1, b2, b3] # zip(A_row, B_col) 返回 (a1, b1), (a2, b2), 以此类推
如果 i = j = 1,则表达式会返回矩阵 C 的元素 c_11。通过这种方式,可以获得一行中的一个元素。
第二步:在矩阵 C 中构建一行
我们的下一个目标是构建一整行。
对于矩阵 A 中的第 1 行,你必须遍历矩阵 B 中的所有列,以在矩阵 C 中获得完整的一行。
回到列表推导式的模板。
- 用第一步中的表达式替换 <要做的操作>,因为它才是我们想要做的。
- 接下来,用 B_col 替换 <项目>,B_col 表示矩阵 B 中的每一列。
- 最后,用 zip(*B) 替换 <可迭代对象>,zip(*B) 表示一个包含矩阵 B 中所有列的列表。
这是第一个列表推导式。
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * 是解包运算符 # zip(*B) 返回矩阵 B 中列的列表
第三步:构建所有行并获得矩阵 C
接下来,你需要通过计算其余的行来填充结果矩阵 C。
为此,你必须遍历矩阵 A 中的所有行。
再次回到列表推导式,然后执行以下操作:
- 用第二步中的列表推导式替换 <要做的操作>。回想一下,在上一步中,我们计算了一整行。
- 现在,用 A_row 替换 <项目>,A_row 代表矩阵 A 中的每一行。
- <可迭代对象> 就是矩阵 A 本身,因为我们正在遍历它的行。
这就是我们最终的嵌套列表推导式!🎉
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
是时候验证结果了! ✔
# 使用 np.array() 转换为 NumPy 数组
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# 输出:
[[ 89 107]
[ 47 49]
[ 40 44]]
仔细观察,你会发现这与我们之前的嵌套 for 循环等效,只不过它更加简洁。
你还可以使用一些内置函数来更有效地执行此操作。 让我们在下一节中探讨它们。
在 Python 中使用 NumPy 的 matmul() 函数进行矩阵乘法
np.matmul() 函数接受两个矩阵作为输入,如果输入的两个矩阵之间的矩阵乘法有效,则返回结果矩阵。
C = np.matmul(A,B) print(C) # 输出: [[ 89 107] [ 47 49] [ 40 44]]
请注意,这种方法比我们之前学习的两种方法更简单。实际上,你可以使用等效的 @ 运算符来代替 np.matmul(),我们接下来会看到。
如何在 Python 中使用 @ 运算符进行矩阵乘法
在 Python 中,@ 是用于矩阵乘法的二元运算符。
它对两个矩阵(通常是 N 维 NumPy 数组)进行操作,并返回结果矩阵。
注意:你需要 Python 3.5 或更高版本才能使用 @ 运算符。
以下是如何使用它:
C = A @ B
print(C)
# 输出
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
请注意,结果矩阵 C 与我们之前得到的结果相同。
可以使用 np.dot() 进行矩阵乘法吗?
如果你曾经遇到过使用 np.dot() 来执行矩阵乘法的代码,那么它是这样工作的。
C = np.dot(A,B) print(C) # 输出: [[ 89 107] [ 47 49] [ 40 44]]
你将看到 np.dot(A, B) 也返回了预期的结果矩阵。
但是,根据 NumPy 文档,你应该只使用 np.dot() 来计算两个一维向量的点积,而不是用于矩阵乘法。
回想一下上一节,结果矩阵 C 中索引位置 (i, j) 处的元素,是矩阵 A 的第 i 行与矩阵 B 的第 j 列的点积。
由于 NumPy 会将此点积运算隐式广播到所有行和所有列,因此你将获得结果矩阵。但是,为了保持代码的可读性并避免歧义,请改用 np.matmul() 或 @ 运算符。
结论
🎯 在本教程中,你学习了以下内容:
- 矩阵乘法有效的条件:矩阵 A 的列数 = 矩阵 B 的行数。
- 如何编写一个自定义 Python 函数来检查矩阵乘法是否有效并返回结果矩阵。函数体使用嵌套的 for 循环。
- 接下来,你学习了如何使用嵌套列表推导式来实现矩阵乘法。它们比 for 循环更简洁,但可能会影响可读性。
- 最后,你学会了如何使用 NumPy 内置的函数 np.matmul() 来进行矩阵乘法,以及这种方法在速度方面如何最有效。
- 你还了解了如何在 Python 中使用 @ 运算符将两个矩阵相乘。
至此,我们关于 Python 中矩阵乘法的讨论就结束了。接下来,你可以学习如何在 Python 中检查一个数字是否为素数,或者解决一些有趣的 Python 字符串相关问题。
祝你学习愉快!🎉