算法排序详解
排序是编程中一项基础且常见的任务。然而,如果选择的排序算法不当,排序过程可能会耗费大量时间。
本文将深入探讨各种不同的排序算法,并提供详细的步骤说明,以及使用Python进行的实现示例。掌握了算法原理后,您可以轻松地将其转换为任何编程语言,因为语言之间的差异主要在于语法方面。
在本教程中,我们将由最慢到最快的顺序介绍各种排序算法,所以请不用担心,跟随文章的指引逐步学习并实践它们吧。
让我们开始探索这些排序算法吧!
插入排序
插入排序是一种简单直观的排序算法,易于实现,但对于大型数组来说,效率较低。它通常不适用于大型数据集的排序。
插入排序的核心思想是将待排序的数组分为已排序部分和未排序部分。初始状态下,已排序部分仅包含数组的第一个元素。算法会从未排序的部分中逐个取出元素,并将其插入到已排序部分的正确位置。
下面我们通过一个示例来直观地展示插入排序的过程:
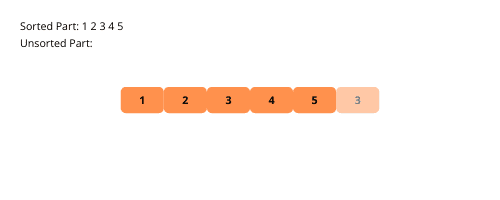
以下是实现插入排序的详细步骤:
- 首先,初始化一个包含虚拟数据(整数)的数组。
- 从数组的第二个元素开始遍历:
- 将当前元素的值及其位置分别存储在变量中。
- 创建一个循环,该循环持续迭代,直到到达数组的起始位置,或者遇到一个小于当前元素的元素。
- 将当前元素之前位置的元素移动到当前元素的位置。
- 将当前位置向前移动一位。
- 循环结束后,当前位置要么位于数组的开头,要么找到了一个小于当前元素的元素。此时,将当前元素放置到当前位置。
插入排序的时间复杂度为O(n²),空间复杂度为O(1)。
至此,我们已经成功对数组进行了排序。接下来,请运行以下Python代码。如果您的计算机尚未安装Python,请参考相关安装指南。您也可以使用在线Python编译器进行测试:
def insertion_sort(arr, n):
for i in range(1, n):
# 当前位置和元素
current_position = i
current_element = arr[i]
# 循环迭代,直到到达数组开头或找到小于当前元素的元素
while current_position > 0 and current_element < arr[current_position - 1]:
# 将前一个元素移动到当前位置
arr[current_position] = arr[current_position - 1]
# 将当前位置向前移动一位
current_position -= 1
# 将当前元素放置到正确位置
arr[current_position] = current_element
if __name__ == '__main__':
# 初始化数组
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
# 打印排序后的数组
print(str(arr))
选择排序
选择排序与插入排序类似,但略有不同。该算法也同样将数组分为已排序和未排序两部分。在每次迭代中,算法会从未排序部分中找到最小的元素,并将其放置到已排序部分的末尾。
以下是通过示例来说明选择排序的步骤:
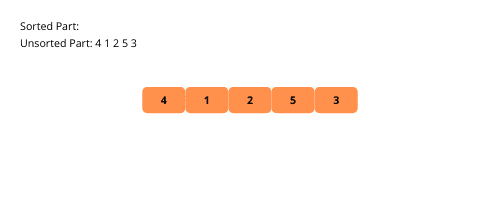
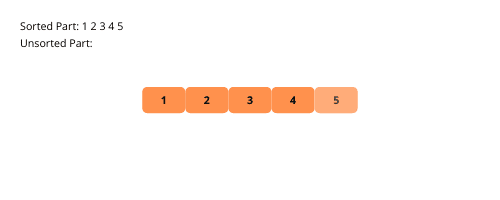
以下是实现选择排序的步骤:
- 首先,初始化一个包含虚拟数据(整数)的数组。
- 遍历给定的数组:
- 维护一个变量,用于存储最小元素的索引。
- 创建一个循环,从当前元素迭代到最后一个元素。
- 检查当前元素是否小于当前最小元素。
- 如果当前元素小于最小元素,则更新最小元素的索引。
- 得到最小元素的索引后,将当前元素与最小元素交换。
选择排序的时间复杂度为O(n²),空间复杂度为O(1)。
尝试自行实现该算法,因为它与插入排序相似。以下是代码示例:
def selection_sort(arr, n):
for i in range(n):
# 存储最小元素的索引
min_element_index = i
for j in range(i + 1, n):
# 检查并更新最小元素的索引
if arr[j] < arr[min_element_index]:
min_element_index = j
# 将当前元素与最小元素交换
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
# 初始化数组
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
# 打印排序后的数组
print(str(arr))
冒泡排序
冒泡排序是一种简单的排序算法,它通过不断地交换相邻的元素来完成排序,直到数组中的元素按顺序排列。
算法会遍历数组,将当前元素与其下一个位置的元素进行比较,如果当前元素大于下一个元素,则交换它们的位置。
通过以下示例可以更直观地理解冒泡排序的过程:
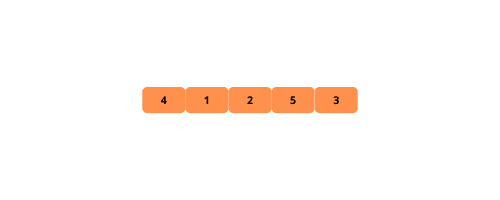
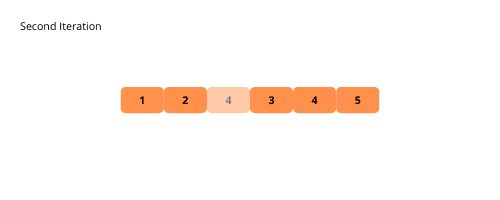
以下是实现冒泡排序的详细步骤:
冒泡排序的时间复杂度为O(n²),空间复杂度为O(1)。
现在,您应该可以轻松地实现冒泡排序了。以下是代码示例:
def bubble_sort(arr, n):
for i in range(n):
# 从0迭代到n-i-1,因为最后i个元素已经排序
for j in range(n - i - 1):
# 检查下一个元素
if arr[j] > arr[j + 1]:
# 交换相邻元素
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
# 初始化数组
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
# 打印排序后的数组
print(str(arr))
归并排序
归并排序是一种递归排序算法,它比前面介绍的算法效率更高。它采用“分而治之”的策略。
归并排序算法将数组递归地划分为两个子数组,分别对它们进行排序,然后将这两个已排序的子数组合并成一个排序的数组。
由于它是一种递归算法,它会不断划分数组,直到子数组变得足够简单(只有一个元素的数组),此时子数组本身就是已排序的。
现在,让我们通过示例来更清晰地理解归并排序的过程:
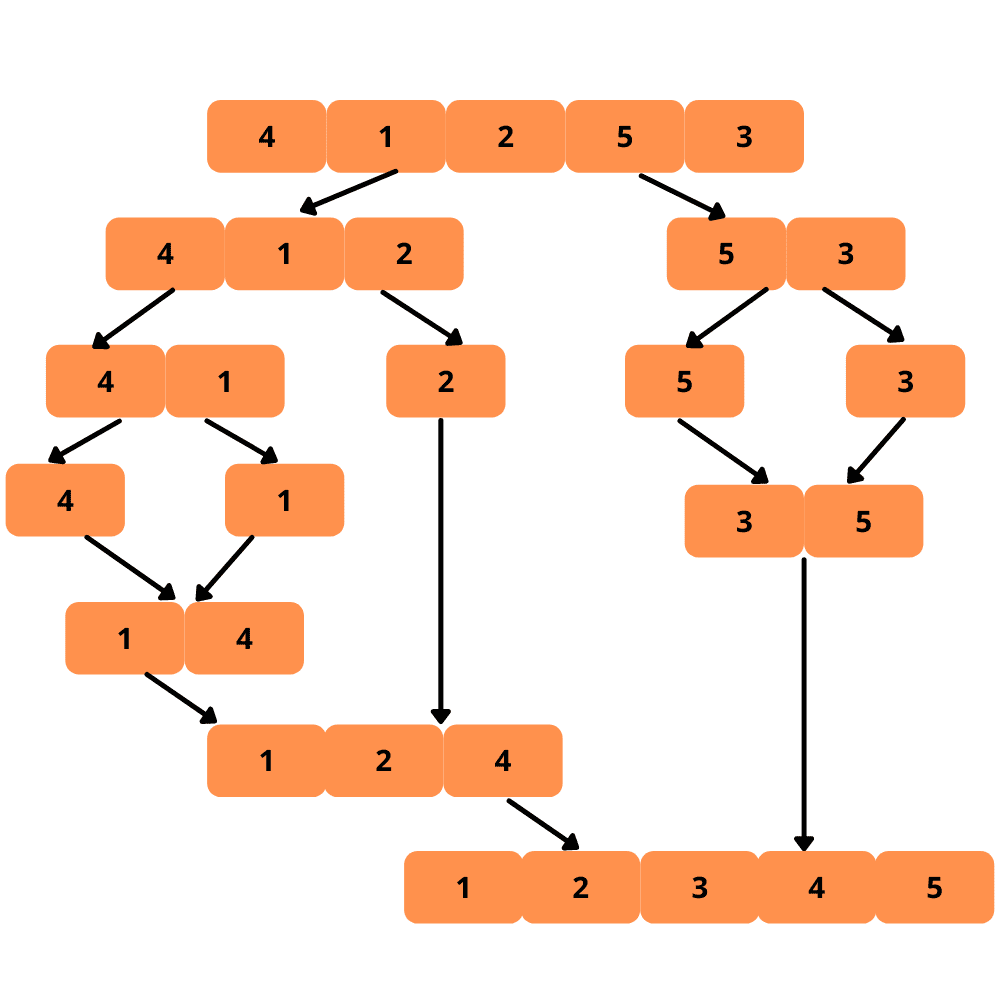
以下是实现归并排序的详细步骤:
- 首先,初始化一个包含虚拟数据(整数)的数组。
- 创建一个名为
merge的函数,该函数负责将两个已排序的子数组合并成一个排序数组。该函数接受数组、左索引、中间索引和右索引作为参数。- 根据给定的索引获取左子数组和右子数组的长度。
- 将数组中的元素复制到相应的左右子数组。
- 遍历两个子数组:
- 比较两个子数组的元素。
- 将两个子数组中较小的元素添加到排序数组中。
- 检查两个子数组中是否还剩余元素,并将它们添加到排序数组中。
- 创建一个名为
merge_sort的函数,该函数接受数组、左索引和右索引作为参数。- 如果左索引大于等于右索引,则直接返回(递归终止条件)。
- 找到数组的中间索引,将数组划分为两个子数组。
- 递归地调用
merge_sort函数,分别对左右子数组进行排序。 - 在递归调用返回后,使用
merge函数合并两个已排序的子数组。
归并排序的时间复杂度为O(n log n),空间复杂度为O(n)。
这就是归并排序算法的实现方式。以下是相应的代码示例:
def merge(arr, left_index, mid_index, right_index):
# 左子数组和右子数组
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
# 获取左右子数组的长度
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
# 合并两个数组的索引
i = j = 0
# 数组元素替换的索引
k = left_index
# 遍历两个子数组
while i < left_array_length and j < right_array_length:
# 比较左右子数组的元素
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
# 添加左子数组和右子数组的剩余元素
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
arr[k] = right_array[j]
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
# 递归函数的基准情况
if left_index >= right_index:
return
# 找到中间索引
mid_index = (left_index + right_index) // 2
# 递归调用
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
# 合并两个子数组
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
# 初始化数组
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
# 打印排序后的数组
print(str(arr))
总结
除了本文中介绍的排序算法之外,还有许多其他的排序算法,但以上是一些最常用的算法。希望您喜欢排序算法的学习过程。
接下来,可以学习有关搜索算法的相关内容。
祝您编程愉快! 🙂👨💻