解密基于格的密码学:一种新颖的信息安全方法
基于格的密码技术是利用一系列数学公式来保障信息安全的有效途径。
密码学包含多种形式,其核心是使用一系列代码来加密数据。长期以来,加密方案等加密工具的设计往往是临时性的,其安全性完全依赖于经验和直觉。
此外,传统加密代码更容易被破解,这使得数据保护成为一个挑战,尤其对那些依赖于传统代码安全设计的人而言。现有的密码学标准也存在不足,量子计算机的发展可能会进一步削弱这些标准,从而加剧安全风险。
因此,对个人信息进行加密已成为当务之急。我们需要一种全新的思路或技术,能够抵御任何形式的破解,即使面对量子计算机也能保护数据。经过深思熟虑,一种新的方法应运而生,这就是基于格的密码学。
本文将探讨基于格的密码学,包括其重要性、工作原理等。
让我们开始吧!
什么是密码学?
密码学是一种利用各种代码保护通信和信息安全的技术,确保只有授权人员才能读取和处理信息,从而防止未经授权的数据访问。
“密码学”一词源于两个词的组合——“crypt”和“writing”,其中“crypt”意为“隐藏”,“graphy”意为“书写”。
用于保护信息的方法基于不同的数学概念和规则计算,通过算法将消息转化为难以解码的难题。密码学主要分为以下三种类型:
- 对称密钥密码学:这是一种加密系统,允许消息的发送者和接收者使用单个密钥对消息进行编码和解码。该方法相对简单快捷。
- 哈希函数:在此算法中,无需使用密钥。哈希值以明文形式计算,且内容难以恢复。各种操作系统都使用此方法来加密密码。
- 非对称密钥密码学:此技术使用一对密钥来编码和解码信息,一个用于加密,另一个用于解密。第一个密钥是公开的,而第二个密钥是只有接收者知道的私钥。
什么是基于格的密码学?
基于格的密码学是一个术语,指构建涉及格的密码算法。它被用于后量子密码学,以保护信息。与已知的公共方案不同,基于格的方案具有更强的弹性,可以抵御来自量子计算机的攻击。
格在基于格的密码学中至关重要。它类似于方格纸上的网格,由一组交叉的点构成。格不是有限的,它定义了一种可以无限延伸的模式。一组点被称为向量,你可以对其中的数字进行任意整数倍的加法。困难之处在于从这个无限网格中找到接近某个点(例如0)的点。
此外,基于格的密码学使用复杂的数学问题来加密数据,使得攻击者难以解决这些问题并窃取数据。
基于格的密码学的历史可以追溯到1996年,由Miklos Ajtai首次提出,其安全性基于格问题。1998年,Joseph H. Silverman、Jill Pipher 和 Jeffrey Hoofstein引入了基于格的公钥加密方案,但该方案相对容易破解。最终,在2005年,Oded Regev推出了第一个公钥加密方案,该方案被证明即使在最坏的情况下也能承受攻击。
此后,不断有研究工作致力于提高原始加密方案的效率。2009年,Craig Gentry提出了第一个基于复格问题的同态加密方案。
例如:CRYSTALS-Dilithium(数字签名算法)和 CRYSTALS-KYBER(公钥加密和密钥建立算法)。
基于格的密码学是如何工作的?
为了理解基于格的密码学的工作原理,我们需要了解一些重要术语:
- 格:格可以被看作一组无限数量的点的规则间隔网格。
- 向量:向量是点的名称,其上的数字称为坐标。例如,(2,3) 是一个具有两个坐标(2和3)的向量。格是这些向量在无限序列中的集合。
- 基:由于格的对象较大,而计算机的内存量有限,数学家和密码学家采用了一种简洁的方式来使用格,即使用格的“基”。基是向量的集合,用于表示形成格的网格中的任何点。
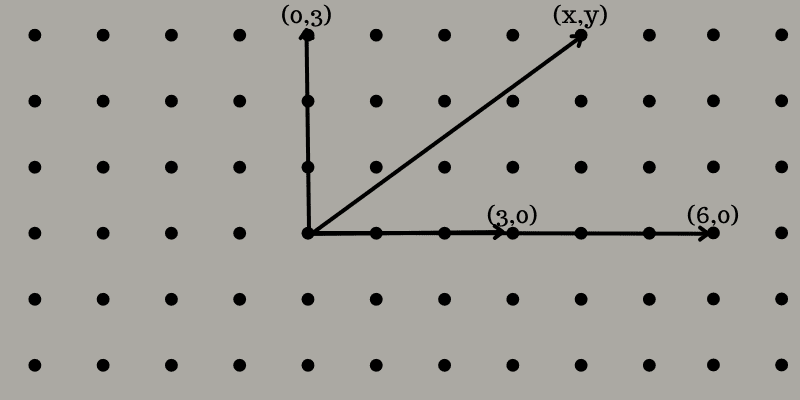
现在,让我们以二维点阵为例,以便更容易理解这个概念。想象一个平面,上面有一个点网格。我们选择两个或多个不位于穿过原点的直线上的点。例如,我们选择(3,0)和(0,3)。要使用这些点生成第三个点,我们需要选择两个整数,例如2和-1。将(3,0)的坐标乘以2得到(6,0),将(0,3)乘以-1得到(0,-3)。将结果点相加得到(6,-3)。通过这种方法,我们可以生成整个点网格,其中点在垂直和水平方向上均匀分布。我们可以将坐标命名为(x,y),其中x和y都是偶数,包括0。
格分为三类:
- 非周期性:非周期性格是一种不完全重复的图案,但没有重叠和间隙。
- 混沌的:混沌格是一种具有重叠和间隙的模式,在方程式中引入了随机性。
- 周期性:周期性格是一种一次又一次重复的图案,没有重叠和间隙。
每个格都作为一种模式工作,只有知道向量的格才能解密消息。由于其图案较多,攻击者很难找到解密的原点和密钥。无论格中有10个点还是100个点,只有拥有正确密钥的人才能解密信息。
如果要求攻击者随机选择两个点,他们很难确定10点格中的哪个点导致了100点格。因此,如果知道密钥,就可以轻松解码消息。
基于格的密码学的优势
基于格的密码学为个人和企业提供了诸多优势。

降低能源消耗
能源消耗随着系统使用量的增加而增加。尽管速度更快,但与其他加密方案相比,基于格的密码学消耗的能量更少。这是因为基于格的密码学是在硬件中实现的,从而降低了功耗。例如,在使用基于格的密码学时,专为加密货币挖掘设计的处理器比传统处理器更节能。
高速计算
与其他密码算法不同,基于格的加密方案的计算速度要快得多。更快的计算时间提高了性能,从而提供更好的实时响应,例如在线游戏或流媒体。
易于实施且灵活
如今,企业正在寻找灵活的选择并节省时间。基于格的密码学易于实施,因为它需要的资源较少并且易于访问。您还可以轻松地在现成的硬件上实现它。此外,基于格的密码学可用于多种应用,例如数字签名、密钥交换和基于密码的加密。不要局限于一种设计,可以用不同的方式构建格子,这提供了很大的灵活性。
合理的密钥大小
基于格的加密密钥大小很小,但不像经典加密算法或基于量子安全同源方案那样小。因此,可以在标准协议中使用这些密钥。
用途广泛

格允许用户解决各种安全挑战,包括签名和密钥协议方案等实用构造。此外,还可以构建跨组织的安全通道,以保护每个人的数据,例如全同态加密和基于身份的加密。
数学基础
由于该算法完全基于数学问题,除非知道密钥,否则很难得到真正的解决方案。这为个人和专业人士的信息安全提供了保证。
易于理解
基于格的密码学中使用的算法基于简单的线性代数,只需要较少的数学背景即可理解其工作原理。因此,您可以立即实施,获得快速的安全性和效率。
学习资源
如果您想了解更多技术知识,以下是一些可供参考的书籍和课程。这些资源都可以在网上找到,可以帮助您深入了解这种安全方法。

#1. 基于格的密码系统:设计视角
本书的作者Jiang Zhang和Zhenfeng Zhang专注于基于格的密码系统,这些系统被广泛认为是很有前景的后量子密码方案。本书提供了关于如何从硬格问题中正确构建安全层的基本见解。主要概念是让您了解可用于选择设计密码系统的格的工具,包括基于属性的加密、数字签名、密钥更改、基于身份的加密和公钥加密。
#2. 硬件中基于格的公钥加密
本书由Sujoy Sinha Roy和Ingrid Verbauwhede合著。他们阐述了公钥加密的实现效率如何解决连接设备网络生成的大量数据的关键安全挑战,这些设备包括微型射频识别标签、台式机等。作者还研究了后量子同态加密和公钥加密方案的实现。
#3. 格及其在密码学中的应用:
这不是一本书,而是Merve Cakir在2014年撰写的论文,同时她继续攻读计算机工程专业的学士学位。这篇论文旨在确定基于格的密码系统的特性,以及随着量子计算机的出现,签名和加密方案的使用变得如何不安全。作者提出了一种基于格问题最坏情况的替代密码学,并通过提供复杂性理论、公钥密码学和线性代数之间的协作来分析计算问题的难度和安全性。
#4. 基础到高级密码学
本课程由Udemy推出,让您对密码学和一些相关术语有清晰的认识。您将学习密码学、散列法、破解和破解代码、密码分析和加密解密。课程包含5个部分和17个讲座,总时长为2小时7分钟。注册此课程,您只需要具备计算机和高中数学的基本知识。
结论
密码学是一种简单但功能强大的工具,可以保护您系统中保存的信息。它通过复杂的数学问题和不同的算法来保护数据,而这正是当今每个人的主要目标。基于格的密码学是最安全的安全机制之一,它使用简单的线性代数来加密数据。它包括用于构建硬模式的格、向量和基。解密方法取决于模式,为此您需要知道原点。如果您拥有密钥,就可以轻松解密数据。
因此,基于格的密码学是一种经过验证的技术,可以保护从IT和安全服务公司到金融等多个行业的个人和企业的数据。 您也可以阅读云密码学。