本指南将引导你了解如何在 Python 中运用 NumPy 的 linspace() 函数,创建一个间隔均匀的数字序列。
你将掌握 linspace() 函数的用法,并通过实例学习如何有效地利用它。
温馨提示:为了顺利学习本教程,请确保你的环境中已安装 Python 和 NumPy 库。
还没有安装 NumPy 吗?别担心,我们为你准备了一份快速安装指南。
准备好开始了吗?让我们开始吧!
NumPy 的安装与导入
在正式开始学习之前,我们先快速完成 NumPy 库的安装步骤。
⏩ 如果你已经安装了 NumPy,可以直接跳到下一部分。
- 如果你正在使用 Google Colab,这是一款基于云端的 Jupyter 笔记本环境,你可以直接导入 NumPy 并开始编写代码(本教程强烈推荐使用 ✅)。
- 如果你希望搭建本地开发环境,我推荐安装 Anaconda 发行版的 Python。Anaconda 自带多个实用软件包。你可以下载适合你操作系统的安装程序。安装过程仅需几分钟 ⌛。
- 即使你的计算机已经安装了 Python,你仍然可以选择安装 Anaconda 发行版。 你可以通过 conda 或 pip 来管理和安装软件包。你可以从 Anaconda 命令提示符运行以下命令来安装 NumPy。
# 使用 conda 安装 NumPy conda install numpy # 使用 pip 安装 NumPy pip install numpy
接下来,通过运行以下命令,以别名 np 导入 NumPy。这样做可以让你在后续代码中用 np 来代替 numpy,避免每次调用模块中的函数时都必须输入完整的名称。
import numpy as np
接下来,我们将采用点符号来调用 NumPy 库中的所有函数,格式为:np.函数名。
为何需要均匀间隔的数字
当使用 NumPy 数组时,经常需要在某个区间内生成一组间隔相等的数字。
在深入探讨之前,我们先来简单回顾一下另一个相似的函数:np.arange()。
NumPy linspace() 与 NumPy arange() 的比较
如果你曾经使用过 NumPy,你或许用过 np.arange() 来创建指定范围内的数字数组。
你知道 np.arange(start, stop, step) 会返回一个从 start 开始,以 step 为步长,直到但不包含 stop 的数字数组;默认步长为 1。
然而,step 的值有时并不容易确定。让我们看几个例子。
例如,如果你需要 4 个介于 0 和 1 之间的等距数字,你很清楚步长应该是 0.25。但如果使用 np.arange(),由于它不包含 stop 值 1,你必须选择一个稍微超出 stop 的值。
下图展示了更多例子,其中你需要在一个区间 [a, b] 中生成特定数量的均匀分布的点。
区间内均匀分布的点
我们的第一个例子,在 [0, 1] 区间生成 4 个均匀分布的点,非常直接。 你知道点之间的步长应该是 0.25。
假设遇到更复杂的情况,你需要列出 1 到 33 之间 7 个均匀分布的点。这时,步长就没那么容易看出来了。当然,你仍然可以手动计算出 step 的值。
但是,np.linspace() 可以让这一切变得更简单! 😄

当使用 np.linspace() 时,你只需指定区间内的点数,无需担心步长。 你将得到一个符合你要求的数组。
鉴于此,让我们在下一部分继续学习 NumPy linspace() 的语法。
NumPy linspace() 的语法
NumPy linspace() 的语法如下所示:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)
一开始,这个语法看起来可能有些复杂,参数很多。
但实际上,大多数参数都是可选的,稍后我们将给出一个更简洁的语法。
现在,让我们逐一解析以上参数:
start和stop分别是区间的起始值和终止值。它们都可以是标量或者数组。在本教程中,我们只考虑标量类型的起始值和终止值。num是区间中均匀分布的点的数量。这是一个可选参数,默认为 50。endpoint也是一个可选参数,可以是True或False。- 默认值为
True,表示包含区间的终点。你可以将其设置为False来排除终点。 retstep是另一个可选参数,接受布尔值True或False。当设置为True时,它会返回步长值。dtype是数组中数字的数据类型。该类型通常被推断为浮点数,一般不需要显式指定。axis是另一个可选参数,表示存储数字的轴。只有当起始值和终止值本身是数组时,这个参数才有效。
▶️ 那么 np.linspace() 返回什么呢?
它返回一个由均匀分布的数字组成的一维数组。如果参数 retstep 设置为 True,它还会返回步长。
根据上述讨论,以下是使用 np.linspace() 的简化语法:
np.linspace(start, stop, num)
上述代码行将返回一个由区间 [start, stop] 中 num 个均匀分布的数字组成的数组。
既然你已经了解了语法,让我们开始编写一些示例。
如何用 NumPy linspace() 创建等间距数组
#1. 作为第一个示例,让我们创建一个由 20 个均匀分布的数字组成的数组,这些数字位于区间 [1, 5] 内。
你可以将 start、stop 和 num 的值指定为关键字参数。 这在下面的代码单元中展示:
import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # 输出: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]
请注意,数组中的数字是从 1 开始到 5 结束的,包括两个端点。 此外,观察到数字(包括 1 和 5)在返回的数组中表示为浮点数。
#2. 在前面的示例中,你将 start、stop 和 num 的值作为关键字参数传入。 如果你以正确的顺序传入参数,你也可以将它们用作仅具有值的位置参数,如下所示。
import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # 输出: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]
#3. 现在,让我们创建另一个数组,并将 retstep 设置为 True。
这意味着该函数现在将返回数组和步长。 我们可以将它们解包为两个变量:arr3(数组)和 step_size(返回的步长)。
以下代码单元说明了如何操作。
import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # 输出: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # 输出: print(step_size) 0.21052631578947367
#4. 作为最后一个示例,让我们将 endpoint 设置为 False,看看会发生什么。
import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # 输出: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]
在返回的数组中,可以看到包含了 1,而没有包含 5。 数组中的最后一个值是 4.8,但我们仍然有 20 个数字。
到目前为止,我们只生成了均匀间隔的数字数组。 在下一节中,让我们通过绘制这些数字来进行可视化。
如何在区间中绘制均匀间隔的数字
在本节中,我们选择 [10, 15] 作为目标区间。 然后,使用 np.linspace() 生成两个数组,分别包含 8 个和 12 个点。
接下来,我们可以利用 matplotlib 库的绘图功能将它们可视化。
为了更清晰地展示,我们将两个数组,N1 = 8 和 N2 = 12,固定在 y 轴的不同高度上。
下面的代码片段演示了这一点。
import numpy as np
import matplotlib.pyplot as plt
N1 = 8
N2 = 12
a = 10
b = 15
y1 = np.zeros(N1)
y2 = np.zeros(N2)
x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)
plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')
plt.ylim([-1, 1])
plt.title(f'在区间 [{a},{b}] 中均匀分布的数字')
plt.xlabel('区间')
plt.show()
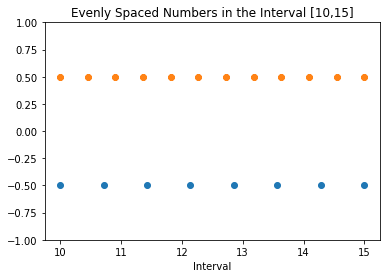
生成均匀分布的点在数学函数的使用中非常有用。我们将在下一节中了解这一点。
如何将 NumPy linspace() 与数学函数一起使用
在使用 np.linspace() 生成均匀间隔的数字数组后,你可以计算该区间内数学函数的值。
在下面的代码单元中,你首先在 0 到 2π 的区间内生成 50 个均匀分布的点。 然后,在数组 x 上使用 np.sin() 创建数组 y。 注意到你可以跳过 num 参数,因为默认值是 50,但为了清晰,我们显式地使用了它。
接下来,你可以在区间 [0, 2π] 内绘制正弦函数。 为此,你可以使用 matplotlib,如同前面的示例。 具体来说,matplotlib.pyplot 中的 plot() 函数用于创建折线图。
import numpy as np
import matplotlib.pyplot as plt
N = 50
a = 0.0
b = 2*np.pi
x = np.linspace(a, b, N)
y = np.sin(x)
plt.plot(x, y, marker = "o")
plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')
plt.show()
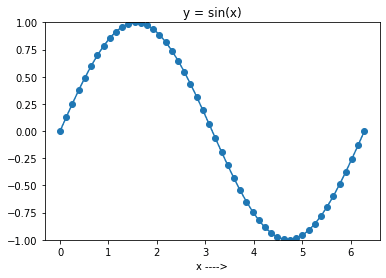
现在,将 N 设置为 10 来运行上述代码。 你将得到如下图所示的图形。
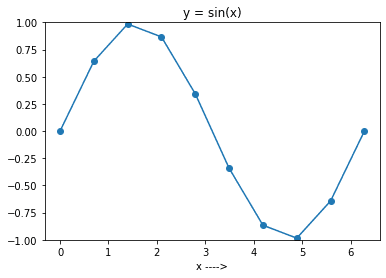
你可以看到,图形不是很平滑,因为你只在区间中选择了 10 个点。
通常,你选择的点越多,函数的图形就越平滑。
总结
以下是我们所学内容的总结。
np.linspace(start, stop, num)返回一个包含区间 [start,stop] 中num个等间距数字的数组。- 将可选参数
endpoint设置为False可以排除stop,区间变为 [start,stop)。 - 可以选择将
retstep设置为True以获取步长值。 - 使用
np.linspace()生成均匀间隔的数组,然后与数学函数一起使用。
我希望你现在对 np.linspace() 的工作原理有了清晰的理解。 你可以选择在 Jupyter 笔记本中运行上述示例。 查看我们的 Jupyter 笔记本指南,或者你可以考虑使用其他 Jupyter 的替代品。
期待在另一篇 Python 教程中再次与你相遇。 在此之前,请继续编码! 😀