数据排序的重要性及其在 JavaScript 中的应用
在应用程序开发中,对数据列表进行排序是至关重要的环节。它不仅有助于数据的呈现,还能优化搜索效率。 因此,对于任何软件工程师而言,掌握数组排序算法是必备技能。 本文将深入探讨 JavaScript 中几种常见的数组排序方法。
什么是排序?它为何如此重要?

图像来源:Unsplash
排序指的是按照特定规则对数据进行组织的过程,可以是升序或降序排列。在 JavaScript 中对数组进行排序具有重要意义,因为它能使数据呈现更加清晰,例如,用户可能希望优先查看最新上传的文件或按价格排列的商品。此外,排序也是二分查找的前提,这种查找算法仅适用于已排序的数据。
尽管现在有许多函数和库能够简化数据排序操作,但了解排序算法的底层原理对于技术面试或编写底层代码仍然至关重要。
JavaScript 数组排序算法详解
冒泡排序

冒泡排序以其简单易懂而著称。 其基本思想是通过多次遍历数组,不断比较相邻元素,如果顺序错误则交换它们。 每次遍历都将把当前未排序的最大(或最小)元素“冒泡”到正确的位置。
该算法需要执行 n 次遍历,其中 n 为数组中元素的数量。每次遍历都会将数组的右侧逐渐排序。以下是冒泡排序的伪代码:
1. 定义 n 为数组元素的数量
2. 循环 n 次,使用 i 记录循环次数 (在每个循环中执行以下操作)
a. 从数组的第二个元素遍历到第 (n - i) 个元素
b. 如果前一个元素大于当前元素,则交换它们
以下是使用 JavaScript 实现的冒泡排序代码:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
为了更好地理解排序过程,建议在循环中添加 `console.log` 语句,以便查看数组在每次迭代中的变化。
下面的代码段展示了如何在排序函数中添加 `console.log`,并演示了如何对一个小型未排序数组进行排序:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
上述代码的执行结果如下所示:

冒泡排序的时间复杂度为 O(n²),因为它需要执行 n 次遍历,每次遍历都循环遍历数组。因此,当数组规模较大时,其性能表现不佳。但是,由于该算法直接在原数组上修改元素,因此其空间复杂度为 O(1)。
插入排序

插入排序是另一种常用的 JavaScript 数组排序算法。 它将数组视为两个部分:已排序部分和未排序部分。 算法从第二个元素开始,将其与已排序部分进行比较,并将该元素插入到已排序部分的正确位置。重复此过程,直到所有元素都已排序。
以下是插入排序的伪代码:
1. 定义 n 为数组元素的数量
2. 从 1 到 n-1 循环 i (从第二个元素开始)
a. 将当前元素赋值给 currentElement (array[i])
b. 设置 j 为 i - 1
c. 当 j >= 0 且 array[j] > current_element 时
i. 将 array[j] 移动到 array[j+1]
ii. 将 j 减 1
d. 将 array[j+1] 赋值为 current_element
以下是 JavaScript 实现的插入排序代码:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
与冒泡排序类似,添加 `console.log` 语句可以帮助你直观地了解插入排序的执行过程。以下代码片段展示了如何使用 `console.log` 来追踪插入排序的每一步:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
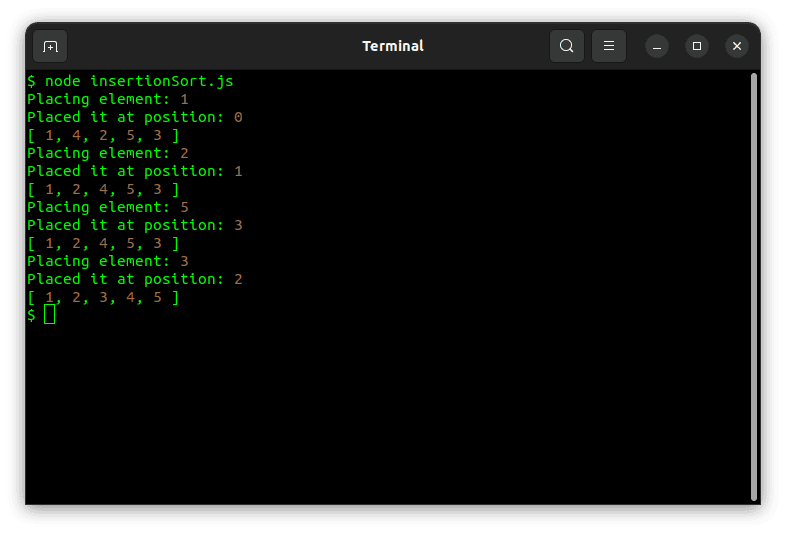
const array = [4, 1, 2, 5, 3];
sort(array);
执行以上代码片段会产生如下结果:
归并排序

与插入排序和冒泡排序的 O(n²) 时间复杂度不同,归并排序的时间复杂度为 O(n log n)。 它是一种更高效的排序算法,尤其适用于大型数据集。
归并排序采用了分治策略。 它首先递归地将数组分割成较小的子数组,直到每个子数组只包含一个元素。 然后,它将这些子数组以排序的方式合并,最终得到一个完全排序的数组。
以下是归并排序的伪代码:
1. 如果数组长度小于等于 1,则返回该数组 (基本情况)
2. 找到中间索引:
a. 将 mid 设置为数组长度除以 2 向下取整的值
3. 将数组分为两个子数组:
a. 创建 leftArray,将数组的前半部分复制到其中 (从索引 0 到 mid)
b. 创建 rightArray,将数组的后半部分复制到其中 (从索引 mid+1 到末尾)
4. 递归地在 leftArray 上调用 MergeSort
5. 递归地在 rightArray 上调用 MergeSort
6. 合并两个已排序的子数组:
a. 创建一个空的 resultArray
b. 当 leftArray 和 rightArray 都不为空时:
i. 如果 leftArray 的第一个元素小于等于 rightArray 的第一个元素,则将其追加到 resultArray
ii. 否则,将 rightArray 的第一个元素追加到 resultArray
c. 将 leftArray 中剩余的元素追加到 resultArray (如果有)
d. 将 rightArray 中剩余的元素追加到 resultArray (如果有)
7. 返回 resultArray
以下是用 JavaScript 实现的归并排序代码:
function sort(array) {
// 基本情况:当数组长度为 1 时停止细分数组
if (array.length == 1) {
return array;
}
// 查找数组的中间点
const m = Math.round(array.length / 2);
// 将数组分成两半
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// 递归调用归并排序
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// 返回一个合并后的已排序数组
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// 合并两个已排序的列表
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
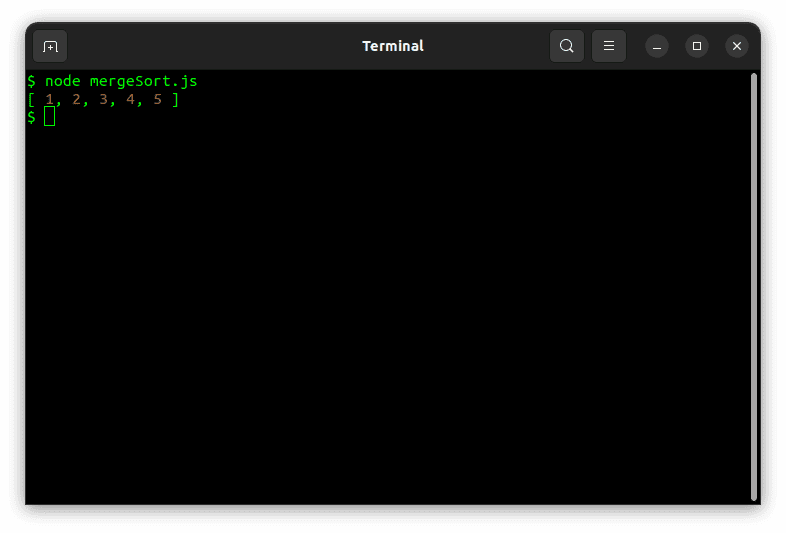
如果使用示例数组运行代码,应该可以得到正确的排序结果。
快速排序

与归并排序类似,快速排序也采用分治策略。 该算法首先选择一个“枢轴”元素,然后将数组中小于枢轴的元素移动到其左侧,将大于枢轴的元素移动到其右侧。 经过这一步骤后,枢轴元素就位于其在已排序数组中的正确位置。
为了围绕枢轴元素移动其他元素,该算法首先将枢轴元素移动到数组的末尾。
然后,使用两个指针,分别从数组的左侧和右侧开始向中间移动。 左指针寻找第一个大于枢轴的元素,右指针寻找第一个小于枢轴的元素。 一旦找到,就交换这两个元素。 重复这个过程,直到左指针超过右指针。
当左右指针停止移动时,交换最后与枢轴元素交换的两个元素中较大的一个。此时,枢轴元素将位于其最终位置,小于枢轴的元素位于其左侧,大于枢轴的元素位于其右侧。
对枢轴元素左侧和右侧的子数组递归地重复以上过程,直到所有子数组都只包含一个元素。
以下是快速排序的伪代码:
1. 如果 lessThanPointer 小于 greaterThanPointer:
a. 从数组中选择一个枢轴元素
b. 移动元素,使小于枢轴的元素位于左侧,大于枢轴的元素位于右侧
c. 递归地在左侧子数组上调用 Quicksort
d. 递归地在右侧子数组上调用 Quicksort
以下是 JavaScript 实现的快速排序代码:
function sort(array, low, high) {
if (low < high) {
// 选择枢轴索引并对数组进行分区
const pivotIndex = move(array, low, high);
// 递归地对枢轴左侧和右侧的子数组进行排序
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// 选择枢轴元素 (在本例中为最后一个元素)
const pivotElement = array[high];
// 初始化较小元素的索引
let i = low - 1;
for (let j = low; j < high; j++) {
// 如果当前元素小于或等于枢轴元素,则将其与索引 i+1 处的元素交换
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// 将枢轴元素交换到其正确的位置
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// 返回枢轴元素的索引
return i + 1;
}
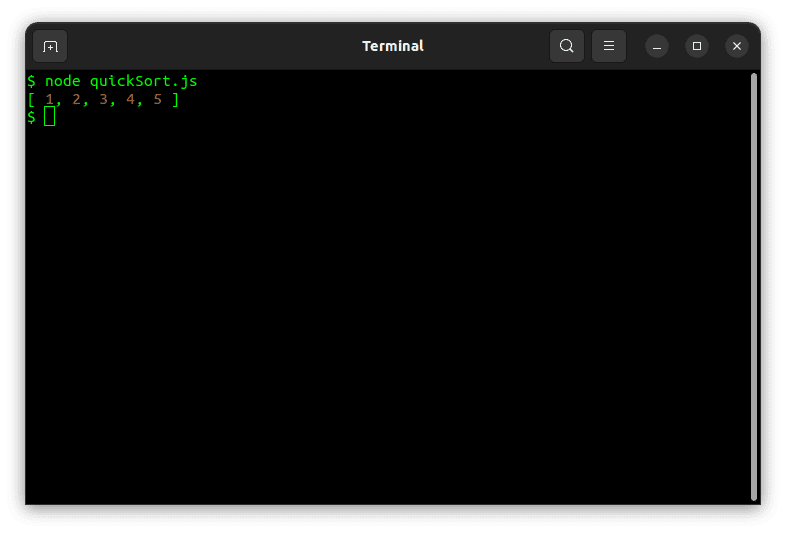
在 Node.js 中使用快速排序对示例数组进行排序应该会产生以下结果:
在最佳情况下,快速排序的时间复杂度为 O(n log n)。 快速排序的空间使用量也呈对数增长。 因此,与其他 JavaScript 数组排序算法相比,它的效率相对较高。
编码面试技巧
❇️练习至关重要。练习不仅能帮助你学习不同的算法,还能培养你的问题解决能力和计算思维能力。 你可以通过 LeetCode 和 AlgoExpert 等平台进行练习。
❇️先尝试独立解决问题。 不要直接跳到解决方案,要尝试自己解决问题,这可以帮助你提升解决问题的能力。
❇️如果某个问题花费了过多的时间,可以参考解决方案。 你仍然可以通过学习解决方案来提高问题解决能力。 大多数学习平台都提供了解决方案。 ChatGPT 和 Google Bard 对于解释概念也很有帮助。
❇️不要急于编写代码。 先在白板上写下你的解决方案,并在编写代码之前仔细考虑。 使用伪代码也可以快速记录你的想法。
结论
在本文中,我们介绍了最常见的一些排序算法。 刚开始学习时,这些算法可能会让人感到难以理解。 因此,我建议大家结合多种资源进行学习,而不是仅仅依赖一种。祝大家编码愉快!
接下来,学习 Python 中的排序函数。