Python 素数检测程序详解
本指南将深入探讨如何利用 Python 编程语言来判断一个数字是否为素数。
在编程面试或测试中,素数检测问题是很常见的。 通过本文,你将掌握解决这类问题的最佳方法。
本教程的主要内容包括:
- 回顾素数的定义和基本概念。
- 使用 Python 编写代码,有效地判断给定数字是否为素数。
- 优化代码,使之达到 O(√n) 的运行时间复杂度。
下面,我们开始详细讲解。
素数的概念
让我们先复习一下素数的基础知识。
在数论中,自然数 n 被定义为素数,如果它仅有两个因数:1 和它本身。 回顾数学知识,如果 i 可以整除 n,那么 i 就是 n 的因数。✅
以下表格列出了一些数字、它们的全部因数以及它们是否为素数。
| 数字 (n) | 因数 | 是否为素数? |
| 1 | 1 | 否 |
| 2 | 1, 2 | 是 |
| 3 | 1, 3 | 是 |
| 4 | 1, 2, 4 | 否 |
| 7 | 1, 7 | 是 |
| 15 | 1, 3, 5, 15 | 否 |
从上表可以得出:
- 2 是最小的素数。
- 1 是任何数字的因数。
- 任何数字 n 都是它自身的因数。
因此,1 和 n 是任何数字 n 的必然因数。素数不应有除了这两个之外的任何其他因数。
这意味着在 2 到 n-1 的范围内,应该找不到任何可以整除 n 而没有余数的非平凡因数。
O(n) 时间复杂度的素数检测算法
现在,我们将上述概念转化为 Python 函数。
可以使用 Python 的 range() 函数来遍历 2 到 n-1 之间的所有数字。
在 Python 中,`range(start, stop, step)` 会返回一个范围对象。你可以遍历这个范围对象,逐步得到从 start 到 stop-1 的序列。
因此,要得到 2 到 n-1 的整数集合,可以使用 `range(2, n)` 并将其结合 `for` 循环。
以下是算法的思路:
- 如果找到任何能整除 n 的数字(余数为 0),即可判断该数字不是素数。
- 如果遍历了 2 到 n-1 的所有数字,而没有找到任何可以整除 n 的数字,则该数字为素数。
Python 素数检测函数
根据上述思路,我们可以定义 `is_prime()` 函数如下:
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
现在来分析一下这个函数定义:
- 函数 `is_prime()` 接收一个正整数 n 作为参数。
- 如果在 (2, n-1) 的范围内找到一个因数,函数返回 `False`,表示该数字不是素数。
- 如果在整个循环中没有找到因数,函数返回 `True`,表示该数字是素数。
接下来,用一些参数调用此函数,验证输出是否正确。
is_prime(2)
# True
is_prime(8)
# False
is_prime(9)
# False
is_prime(11)
# True
输出结果显示,2 和 11 是素数(函数返回 `True`),而 8 和 9 不是素数(函数返回 `False`)。
优化 `is_prime()` 函数
我们可以对函数进行一些优化。观察下表中的因数列表。
| 数字 | 因数 |
| 6 | 1, 2, 3, 6 |
| 10 | 1, 2, 5, 10 |
| 18 | 1, 2, 3, 6, 9, 18 |
我们发现,n 中唯一大于 n/2 的因数是 n 本身。
因此,不必循环到 n-1,只需循环到 n/2 即可。
如果在 n/2 之前没有找到因数,那么在 n/2 之后也不会找到因数。
现在,修改 `is_prime()` 函数以检测 (2, n/2) 范围内的因数:
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
让我们通过函数调用验证输出。
is_prime(9)
# False
is_prime(11)
# True
虽然看起来进行了优化,但从运行时间复杂度来看,此算法与之前的算法效率相同,都是 O(n)。这意味着算法的运行时间与 n 的值成线性关系。
我们还能做得更好吗?答案是肯定的!
▶️ 请继续阅读,了解如何进一步优化素数检测的时间复杂度。
O(√n) 时间复杂度的素数检测算法
一个数的因数总是成对出现。
如果 a 是 n 的因数,那么一定存在另一个因数 b,使得 a × b = n,简而言之,ab = n。
通过示例验证一下:
以下表格展示了数字 18 的成对因数。你可以使用其他数字进行验证。
同时注意,√18 大约为 4.24。
在成对的因数 (a, b) 中,如果 a 小于 4.24,那么 b 一定大于 4.24。例如 (2, 9) 和 (3, 6)。
18 的成对因数:(1,18), (2,9), (3,6)
下图显示了数轴上 18 的因数:
如果数字 n 恰好是一个完全平方数,那么 a = b = √n 就是其中一个因数。
▶️ 观察表格中数字 36 的因数。由于 36 是一个完全平方数,所以 a = b = 6 是其中一个因数。对于其他因数对 (a, b),若 a < 6,则 b > 6。
36 的成对因数:(1,36), (2,18), (3,12), (4,9), (6,6)
总结如下:
- 每个数字 n 都可以写成 n = a × b 的形式。
- 如果 n 是完全平方数,则 a = b = √n。
- 如果 a < b,则 a < √n 且 b > √n。
- 如果 a > b,则 a > √n 且 b < √n。
因此,不必循环到 n/2,只需循环到 √n 即可。这比之前的方法效率高得多。
如何将 `is_prime()` 修改为 O(√n) 算法
现在,优化函数,检测 Python 中的素数。
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
分析上面的函数定义:
- 导入 Python 的内置 `math` 模块,使用 `math.sqrt()` 函数计算平方根。
- 由于 n 可能不是完全平方数,所以必须将其转换为整数,用 `int(var)` 将 `var` 转换为整数。
- 为了确保我们实际上检查到 √n,需要加一,因为 `range()` 函数默认不包含范围的终点。
以下代码单元验证 `is_prime()` 函数是否正常工作。
is_prime(8)
# False
is_prime(15)
# False
is_prime(23)
# True
在下一节中,创建简单的图表,直观理解 O(n) 和 O(√n)。
直观比较 O(n) 和 O(√n)
▶️ 在 Jupyter Notebook 环境中运行以下代码片段:
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
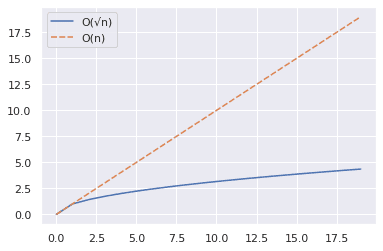
上述代码展示了如何绘制一系列值的 n 和 √n 曲线图。
- 使用 NumPy 的 `arange()` 函数创建一个数字数组。
- 将 20 以内(不包含 20)的 n 和 √n 值收集到 pandas DataFrame 中。
- 使用 seaborn 的 lineplot() 功能绘制图表。
下图显示,√n 明显小于 n。

现在将范围扩大到 2000,重复上述步骤:
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
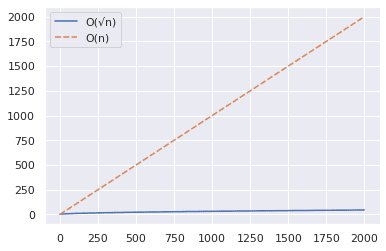
从上图可以看出,在检测较大的数字是否为素数时,O(√n) 算法明显更快。
举一个简单的例子:2377 是一个素数,验证一下!😀
使用 O(n) 方法,需要大约 2000 步,而 O(√n) 算法只需 49 步即可得到答案。✅
结论
⏳ 现在来快速总结一下:
- 检测一个数字是否为素数,最直接的方法是遍历 (2, n-1) 范围内的所有数字。如果没有找到能整除 n 的因数,则 n 为素数。
- 由于 n 大于 n/2 的唯一因数是 n 本身,可以选择只遍历到 n/2。
- 以上两种方法的时间复杂度均为 O(n)。
- 由于一个数的因数总是成对出现,所以最多只需遍历到 √n 即可。此算法比 O(n) 快得多。检测大数是否为素数时,优势非常明显。
希望你掌握了如何在 Python 中检测素数。下一步,你可以查看我们关于 Python 字符串操作的教程,你将学习如何检测字符串是否为回文、字谜等。
下次教程再见。祝你编程愉快!👩🏽💻