探索高效搜索算法
在数据海洋中寻找特定的信息,就像在浩瀚的宇宙中寻找一颗星星,这始终是一项具有挑战性的任务。然而,正如我们在生活中运用直觉和一些“捷径”来寻找物品一样,编程世界中也存在着一些精心设计的模式,它们能够帮助我们高效地定位数据。
在日常生活中,我们的搜索行为通常是随机且无规律的。我们通常会直接前往我们认为最有可能找到目标的位置,而不是遵循某种固定的步骤。那么,这种随性的搜索方式在计算机程序中是否可行呢?
答案是否定的!为了在程序中高效地查找信息,我们需要依靠精心设计的算法,这些算法遵循特定的模式和规则。本文将带您一起探索一些常用的搜索算法,它们在编程领域中发挥着至关重要的作用。
编程世界中有无数的算法,但本文将重点介绍那些最重要和最常用的。掌握这些算法之后,您将更容易理解和学习其他算法。在本文中,“查找”指的是在数组中定位特定元素的操作。
让我们深入了解这些算法吧!
线性搜索:逐一排查
正如其名,线性搜索算法采用一种线性的模式在数组中搜索元素。它从数组的起始位置开始,逐个检查每个元素,直到找到目标元素或遍历完整个数组。一旦找到目标元素,算法将立即停止执行。
为了更好地理解线性搜索算法,我们不妨借助一些生动的例子来帮助说明。
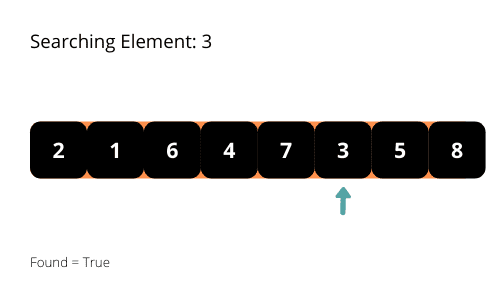
仔细观察搜索的过程,您会发现该算法在最坏的情况下需要遍历整个数组,即时间复杂度为 O(n)。在分析算法时,我们通常需要关注其最坏情况下的时间复杂度。因此,线性搜索算法的时间复杂度为 O(n)。
接下来,让我们看看线性搜索算法的具体实现方式。
线性搜索的实现步骤
现在您应该对线性搜索算法有了一个基本的了解。是时候动手编写代码了!首先,让我们梳理一下实现线性搜索算法的步骤,然后您可以尝试自己编写代码。如果遇到困难,也不用担心,稍后我会提供代码供您参考。
以下是实现线性搜索算法的步骤:
| 1. | 初始化一个包含元素的数组(可以是你喜欢的幸运数字)。 |
| 2. | 编写一个名为 search_element 的函数,该函数接受三个参数:数组、数组的长度以及要搜索的元素。 |
| 3. | 在 search_element 函数中:
|
| 4. | 根据 search_element 函数的返回值,打印相应的消息。 |
根据以上步骤,尝试编写代码来实现线性搜索算法。
您完成线性搜索算法的实现了吗?希望如此!如果完成了,请使用以下代码进行对比,检查您的实现是否正确。如果还没有完成,也没关系,请仔细阅读下面的代码,了解如何实现线性搜索算法,您很快就能掌握它。
## 搜索函数 def search_element(arr, n, element): ## 遍历数组 for i in range(n): ## 检查当前元素是否与目标元素匹配 if arr[i] == element: ## 如果匹配,返回 True return True ## 如果执行到此处,则表示未找到元素 return False if __name__ == '__main__': ## 初始化数组、长度以及要搜索的元素 arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "找到了") else: print(element_to_be_searched, "未找到")
首先,使用数组中存在的元素来运行程序,然后尝试使用数组中不存在的元素来运行程序。观察运行结果,加深理解。
线性搜索算法的时间复杂度为 O(n)。那么,我们是否可以采用其他模式来进一步优化搜索效率呢?
答案是肯定的!接下来,让我们一起看看另一种更高效的搜索算法:二分查找。
二分查找:一分为二,高效搜索
二分查找算法的核心思想是每次检查数组的中间元素。这种算法适用于已排序的数组。二分查找算法不断地将搜索范围缩小一半,直到找到目标元素或确定目标元素不存在为止。
具体来说,二分查找算法首先检查数组的中间元素,如果找到则停止执行。否则,如果中间元素小于目标元素,则忽略中间元素左侧的部分,继续在右侧部分进行搜索;反之,如果中间元素大于目标元素,则忽略中间元素右侧的部分,继续在左侧部分进行搜索。
通过每次迭代都缩小搜索范围,二分查找算法所需的检查次数远少于线性搜索算法。下面通过一些图示来帮助我们更好地理解二分查找算法。
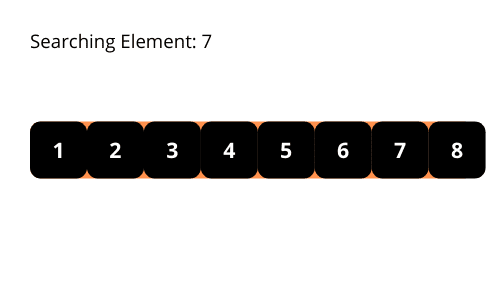
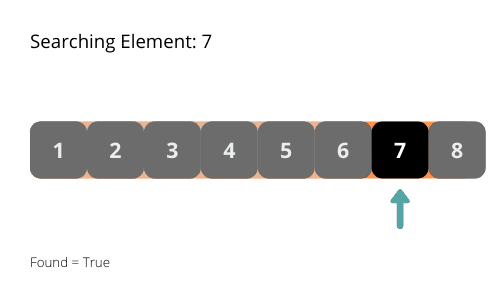
二分查找算法的时间复杂度为 O(log n)。每次迭代都将搜索区域的长度减半,其减少的速度是指数级的。
二分查找的实现步骤
首先,让我们看看实现二分查找算法的步骤,然后再看代码。以下是完成二分查找算法实现的步骤:
| 1. | 初始化一个已排序的数组(可以是您的幸运数字)。 |
| 2. | 编写一个名为 search_element 的函数,该函数接受三个参数:已排序的数组、数组的长度以及要搜索的元素。 |
| 3. | 在 search_element 函数中:
|
| 4. | 根据 search_element 函数的返回值,打印相应的消息。 |
现在,尝试像实现线性搜索算法一样,自己编写代码来实现二分查找算法。
…
您是否完成了代码?
是的!将您的代码与以下代码进行比较,看看是否一致。如果还没有完成,也不用担心,请仔细阅读下面的代码,了解如何实现二分查找算法。
## 搜索函数 def search_element(sorted_arr, n, element): ## 数组迭代索引 i = 0 ## 用于跟踪搜索区域的变量 ## 使用起始和结束索引初始化 start = 0 end = n - 1 ## 遍历数组 while i < n: ## 获取中间元素的索引 middle = (start + end) // 2 ## 检查中间元素是否与目标元素匹配 if sorted_arr[middle] == element: ## 如果数组中存在目标元素,则返回 True return True elif sorted_arr[middle] < element: ## 将搜索区域的起始索引向右移动 start = middle + 1 else: ## 将搜索区域的结束索引向左移动 end = middle - 1 i += 1 return False if __name__ == '__main__': ## 初始化数组、长度以及要搜索的元素 arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "找到了") else: print(element_to_be_searched, "未找到")
在目标元素存在和不存在的两种不同情况下,测试代码的运行结果,加深理解。
结论
二分查找算法比线性搜索算法更加高效。但是,二分查找算法要求数组必须是已排序的,而线性搜索算法则没有这个限制。对数组进行排序需要一定的时间。然而,如果采用高效的排序算法,排序过程与二分查找算法的结合将具有很高的效率。
现在,您对 Python 中最常用的两种搜索算法有了深入的了解。在未来的编程工作中,您可以根据实际情况选择合适的算法来解决问题。
接下来,您可以探索一些流行的自托管搜索软件,进一步拓展知识领域。
祝您编程愉快!🙂🧑💻