深入理解假设检验：方法、应用与优势
假设检验是众多分析师，无论是来自私营企业还是政府部门，都广泛采用的一种重要方法。 它旨在对人口数据做出合理的推断和假设。
如果您日常工作中涉及人口数据的处理和研究，那么您一定不会对假设检验感到陌生。这是一种不可或缺的工具。
虽然存在多种方法来构建假设，但并非所有方法都能保证高精确度。如果在使用数据时缺乏信心，或者数据本身就存在不确定性，那么这可能会给您的组织带来潜在的风险。
因此，采用假设检验是一种明智的策略，它能显著提高数据分析的准确性。它在人口分析中起着至关重要的作用。
本文将深入探讨假设检验的含义、工作原理、优势以及实际应用，希望能帮助您更好地理解这一重要的统计方法。
事不宜迟，让我们开始探索假设检验的世界！
什么是假设检验？
假设检验是一种统计推断方法，它允许分析师评估现有的人口数据是否足以支持特定的假设。通过此方法，分析师可以客观地评估假设，并根据手头的数据来判断其准确性。
简而言之，这是一个基于推论统计的测试流程，它使您能够根据收集到的样本数据对整体人口数据做出判断。
通常情况下，分析师很难获取整个人口的所有属性或特定参数。然而，借助假设检验，您可以基于样本数据及其准确性，做出更明智的预测和决策。
假设检验的类型
假设检验主要包括以下几种类型：
- 零假设（Null Hypothesis）： 这是一种统计声明，它假设样本数据是随机变化的，并且所研究的两个变量之间不存在关联性。
- 备择假设（Alternative Hypothesis）： 它支持研究的主要论点，并与零假设相对立。它是检验过程的核心驱动力，它表明样本数据中两个变量之间存在关联。
- 非定向假设（Non-directional Hypothesis）： 这类假设检验采用双尾检验，它指出样本数据中两个变量之间不存在特定的方向，真实值与预测值可能存在差异。
- 定向假设（Directional Hypothesis）： 定向假设描述了两个变量之间存在某种特定的关系。在这种情况下，样本数据中的一个变量可能会对另一个变量产生影响。
- 统计假设（Statistical Hypothesis）： 它帮助分析师评估数据和数值是否符合特定的假设。它在对样本总体参数的结果进行陈述和假设时非常有用。
接下来，我们来探讨假设检验的具体方法。
假设检验的方法
为了评估某个假设是否成立，作为分析师，您需要收集充分的证据来得出结论。在检验过程中，零假设和备择假设会在评估开始之前建立。
假设检验并非仅依赖单一的方法，而是采用多种方法来评估样本数据是否符合要求。分析师需要考虑数据的性质和样本量，并选择最适合其特定情况的检验方法。
正态性检验（Normality Test）
这是一种标准的假设检验方法，用于分析样本数据是否符合正态分布。在测试过程中，会检查数据点围绕均值的分布情况，看它们是高于还是低于均值。
在正态分布中，数据点高于或低于平均值的可能性是相同的。其图形呈钟形曲线，数据均匀地分布在均值的两侧。
Z检验（Z-Test）
当人口数据呈正态分布时，可以使用Z检验。它用于测试两个独立总体参数的均值之间是否存在差异，前提是已知数据的方差。
在分析人口数据时，如果样本量超过30，通常会使用Z检验。中心极限定理是Z检验适用的另一个原因，该定理指出，随着样本量的增加，样本趋向于正态分布。
T检验（T-Test）
当样本量较小且分布通常呈正态分布时，可以使用T检验。通常，当样本量小于30且不知道参数的标准差时，会应用T检验。
通过T检验，您可以计算特定总体数据的置信区间。
卡方检验（Chi-Square Test）
卡方检验是一种常用的假设检验过程，通常用于评估数据分布的拟合度和完整性。
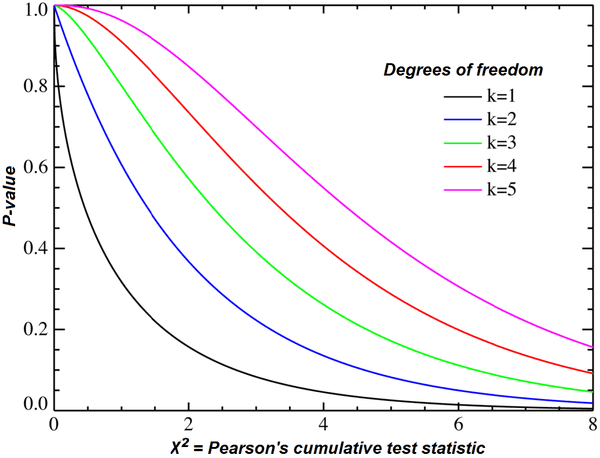来源：wikipedia.org
卡方检验的主要用途是检验总体方差是否与假设值或已知值一致。存在多种卡方检验，但最常见的是方差和独立性的卡方检验。
方差分析（ANOVA）
方差分析是一种统计检验方法，有助于比较两个或多个样本数据集的均值。它还能够解释样本数据的因变量和自变量之间的关系。方差分析的用途与Z检验和T检验类似，但后两者仅限于比较两个均值。
假设检验的工作原理
所有使用假设检验的分析师都会使用随机样本数据进行分析和测量。在检验过程中，随机样本数据用于检验零假设和备择假设。
如前所述，零假设和备择假设是互斥的，在检验结果中，只有一个假设可以为真。
然而，在某些情况下，零假设可能会被拒绝，但备择假设不一定总是正确。
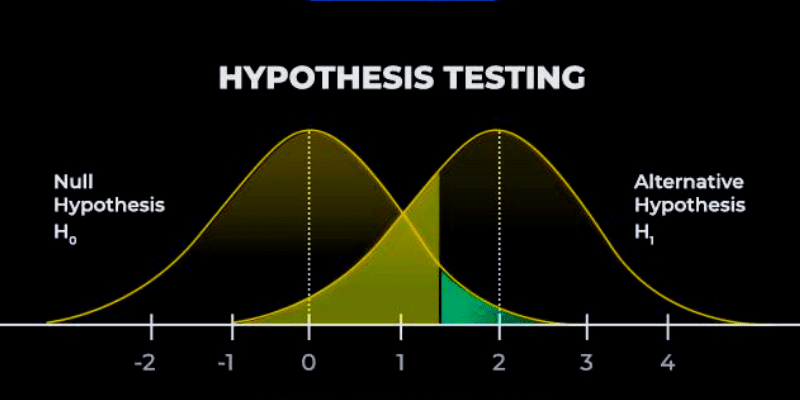资料来源：分析步骤
p值：当测试过程开始时，会涉及p值，它表示结果是否显著。p值还显示了在检验过程中拒绝或不拒绝零假设时发生错误的概率。生成的p值介于0和1之间，并将其与显著性水平（alpha水平）进行比较。
显著性水平定义了在检验期间拒绝零假设时可接受的风险。需要注意的是，假设检验的结果可能导致两种类型的错误：
- 第一类错误（Type I Error）： 当检验结果否定了真实的零假设时发生。
- 第二类错误（Type II Error）： 当检验结果接受了错误的零假设时发生。
导致拒绝零假设的所有值都存储在临界区中。临界值将临界区与其他区域分隔开来。
执行假设检验的步骤
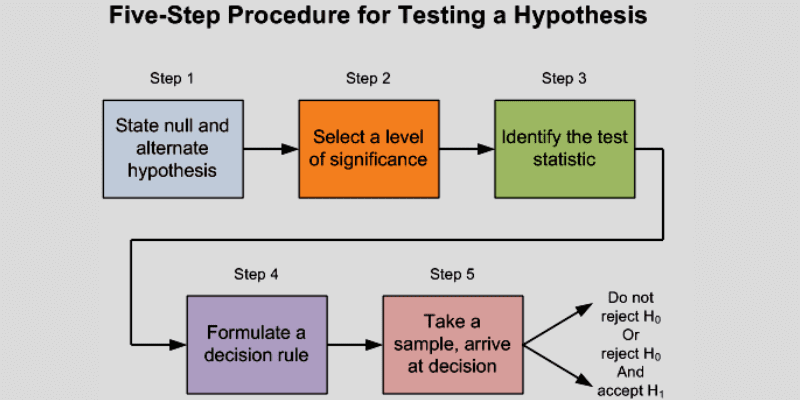资料来源：媒体
假设检验主要包括以下四个步骤：
- 定义假设： 第一步，分析师需要定义零假设和备择假设，确保只有一个假设为真。 例如，零假设可能表明平均BMI没有差异，而备择假设可能表明平均BMI存在显著差异。
- 制定计划： 接下来，需要设计一个关于如何分析示例数据的计划。必须进行抽样和收集样本数据，确保其能支持检验您的假设。
- 分析样本数据： 确定如何评估数据之后，就可以开始分析了。 您必须对示例数据进行仔细分析，避免出现冗余。 分析数据时，应检查样本是否相互独立，并且两个样本的大小是否足够大。
- 计算测试统计数据： 在此阶段，您需要计算测试统计数据并找到p值。 p值将通过假设零假设为真来确定。
- 评估结果： 最后一步是评估假设检验的结果。 您需要根据样本数据来决定是拒绝零假设还是接受其合理性。
接下来，我们将探讨假设检验的优势。
假设检验的优势
假设检验的主要优势包括：
- 它可以帮助您分析您对数据决策的主张的强度。
- 它可以帮助分析师建立一个可靠的环境，以对样本数据做出合理的判断。
- 它可以让您确定假设检验中涉及的样本数据是否具有统计上的显著性。
- 它有助于评估任何系统测试过程中测试结果的可靠性和有效性。
它还可以帮助您将样本阶段的数据外推到更大的总体。
假设检验的应用场景
假设检验被广泛应用于各个领域，以评估样本数据的准确性。以下是一些实际应用案例：
#1. 临床试验
假设检验在临床试验中被广泛使用，帮助医疗专业人员确定新药、治疗方法或程序是否有效。例如，医生可能会假设某种治疗方法可以降低患者的钾水平。
医生在治疗前会测量一组患者的钾水平，并在治疗后再次检查水平。
接下来，医生进行假设检验。零假设(H0)为治疗后钾水平与治疗前相同（Uafter = Ubefore）。备择假设(Ha)则为治疗后钾水平有所下降(Uafter < Ubefore)。
如果p值小于显著性水平，医生可以得出结论，治疗方法有效降低了钾水平。
#2. 制造业
制造工厂使用假设检验来帮助主管判断新方法或技术是否有效。例如，他们可能会使用假设检验来确定新方法是否能减少每批次的缺陷产品数量。假设目前每批次的不良品数量为300件。
制造商需要确定使用新方法前后缺陷产品的平均数量。他们可以进行假设检验，零假设(H0)为使用新方法前后产生的缺陷产品平均数量相同（Uafter = Ubefore）。
备择假设(Ha)为使用新方法后产生的缺陷产品总数不相同（Uafter ≠ Ubefore）。
如果测试后p值小于显著性水平，制造单位可以断定缺陷产品的数量发生了变化。
#3. 农业
假设检验常用于确定肥料或杀虫剂是否对植物的生长和免疫力产生影响。生物学家可以通过测试来证明，施用新肥料后，某种植物的生长高度可能会超过15英寸。
生物学家可能会施肥一个月来收集样本数据。当他们进行测试时，一个假设是H0：U=15英寸，这表明肥料不会促进植物的平均生长。 另一个假设是Ha：U > 15英寸，表明肥料会促进植物的平均生长。 当p值小于显著性水平时，生物学家可以证明肥料确实导致了比以前更多的生长。
学习资源
#1. Udemy的“统计学：逐步介绍”
Udemy提供一门统计学课程，其中包含假设检验的逐步讲解。本课程涵盖了来自前谷歌数据科学家的示例和课程，帮助您掌握置信区间、假设检验等概念。
#2. Udemy的“数据分析的基本统计数据”
这门Udemy的“数据分析基本统计”课程通过真实世界的项目、有趣的活动、假设检验、概率分布、回归分析等内容来帮助您学习统计学。
#3. “数据科学和商业分析统计”
这门由Udemy提供的“数据科学和商业分析统计”课程将帮助您学习假设检验，它涵盖了不同的统计主题，使数据科学家和商业分析师能够学习和掌握相关知识。课程内容包括推论和描述性统计以及回归分析。
#4. Jim Frost的“假设检验”
这本书在亚马逊上有售，是帮助分析师做出数据驱动决策的直观指南。
它涵盖了假设检验的工作原理、为什么要使用假设检验、如何有效地使用置信区间、p值、显著性水平以及更多主题。
#5. Scott Hartshorn的“假设检验”
这本书以其视觉化的示例而著称，特别适合寻求快速入门假设检验的初学者。
它将向您介绍统计数据的重要性、类型及其工作原理。它不需要您具备深厚的统计知识，而是以直观的方式解释所有内容。
结语
假设检验有助于验证假设，并根据评估得出统计结论。它被广泛应用于各个领域，从制造业和农业到临床试验和IT。 这种方法不仅精确，还能帮助您为组织做出基于数据的明智决策。
接下来，您可以了解一下成为商业分析师的学习资源。