Python 中数值数据类型的舍入技巧
在Python中处理数值数据时,掌握各种舍入方法至关重要。无论是传感器读数、货币汇率还是其他类型的数值数据,了解如何精确舍入数值可以提高数据处理的效率和准确性。
现实世界中的数据集通常包含数值和分类特征。数值特征的种类繁多,从传感器读数到汇率、生物医学信号等,无所不包。
在处理数值数据时,你可能需要将数值舍入到特定的精度,原因包括:
- 保证数据格式的一致性。
- 便于数据存储和进一步处理。
本教程将介绍Python中各种舍入方法,包括将数字舍入到指定精度、向上舍入到最接近的整数、向下舍入到最接近的整数等。
让我们开始学习吧!
如何使用内置 round() 函数进行舍入
在Python中最常用的舍入方法是使用内置的 round() 函数。首先,我们来了解它的语法:
round(num, ndigits)
其中:
num是待舍入的数值。ndigits是一个可选参数,默认值为None,表示要将数字舍入到的小数位数。例如,ndigits = 2,则将num舍入到小数点后两位。round()函数返回num舍入到指定精度后的结果。
round() 函数的使用示例
通过一些示例来了解 round() 函数是如何工作的。
如前所述,ndigits 是可选的。因此,当只使用数值调用 round() 时,该数值会被舍入到最接近的整数。
number = 7.123456 rounded = round(number) print(rounded) # 输出:7
现在,我们来看一些指定精度的示例。
当 ndigits 设置为 2 时,数字被舍入到小数点后两位:
number = 7.123456 rounded = round(number, 2) print(rounded) # 输出:7.12
当 ndigits 设置为 3 时,数字被舍入到小数点后三位:
number = 7.123456 rounded = round(number, 3) print(rounded) # 输出:7.123
你也可以使用 round() 函数对负数进行舍入:
number = -3.4 rounded = round(number) print(rounded) # 输出:-3
此处,函数将 -3.4 舍入到最接近的整数 -3。
四舍五入到最接近的十位和百位
你知道 ndigits 也可以取负值吗?
是的,你可以使用负的 ndigits 值调用 round() 函数。 当这样做时,舍入操作将发生在小数点左侧而不是右侧。
这是什么意思? 让我们看一些例子。
当我们将 ndigits 设置为 -1 时,该数字将四舍五入到最接近的十位。
number = 7.123456 rounded = round(number, -1) print(rounded) # 输出:10.0
调用 round() 函数并将 ndigits 设置为 -2 会将数字 77.123456 向上舍入到最接近的百位,在本例中为 100.0。
number = 77.123456 rounded = round(number, -2) print(rounded) # 输出:100.0
到目前为止,round() 函数似乎遵循了我们在学校数学中学到的通用舍入原则。但情况并非总是如此。
存在一些浮点数的限制。 因此,在进行舍入时,你可能会看到一些意想不到的结果。 另一个有趣的注意事项是银行家舍入法。
什么是银行家舍入?
启动 Python REPL 并尝试以下示例:
>>> round(1.5) 2
我们看到 round(1.5) 返回 2(如预期)。 那么 round(2.5) 应该返回什么?
>>> round(2.5) 2
有趣,不是吗? round(1.5) 和 round(2.5) 都返回 2。这是如何以及为什么呢?
在内部,round() 函数的工作原理如下:介于两个整数之间的任何中间值都将舍入到最接近的偶数。 这就是所谓的银行家舍入法,或舍入到一半的偶数策略。
我们知道 round() 函数足以完成简单的舍入任务。 但有时,你可能需要将数字向上或向下舍入到最接近的整数。
那么该怎么做呢? 我们将在下一节中了解这一点。
如何在 Python 中向上舍入数字
要将数字向上舍入到最接近的整数,可以使用:
使用 math.ceil()
ceil() 函数(或上限函数)的工作原理如下:它将数字向上舍入到大于该数字的最小整数。
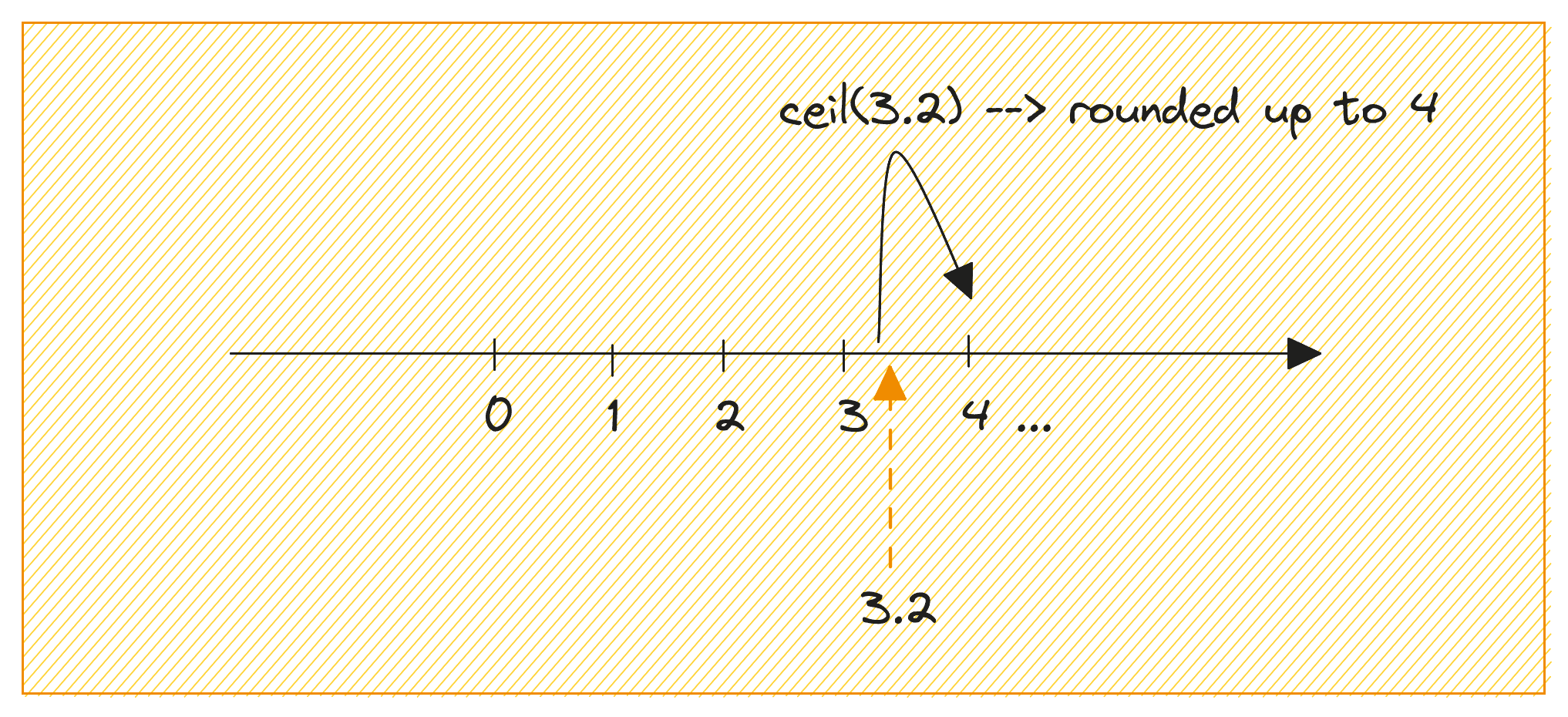
以下代码片段展示了如何使用 ceil() 函数将数字 3.2 向上舍入:
import math number = 3.2 rounded_up = math.ceil(number) print(rounded_up) # 输出:4
使用 decimal 模块
到目前为止,我们使用的是内置的浮点数据类型。 但对于科学计算和金融领域的某些应用程序,我们需要更高的精度。 为此,Python 提供了 decimal 模块,该模块提供:
- 更精确的浮点运算。
- 可靠的相等测试。
- 对精度级别进行更精细的控制(默认精度为 28 位)。
要查看当前上下文,可以使用 getcontext(),如下所示:
from decimal import getcontext current_context = getcontext() print(current_context)
你应该可以看到当前的精度和舍入模式等信息:
# 输出 Context(prec=28, rounding=ROUND_HALF_EVEN, Emin=-999999, Emax=999999, capitals=1, clamp=0, flags=[], traps=[InvalidOperation, DivisionByZero, Overflow])
要向上舍入数字,可以通过指定以下内容来使用 quantize():
- 精度 (
0.0,因为我们想舍入到最接近的整数),以及 - 舍入模式:
ROUND_CEILING。
from decimal import Decimal, ROUND_CEILING
number = Decimal('3.2')
rounded_up = number.quantize(Decimal('0'), rounding=ROUND_CEILING)
print(rounded_up)
# 输出:4
此处,数字 3.2 已向上舍入到最接近的整数 4。
如何在 Python 中向下舍入数字
现在,让我们看看如何在 Python 中向下舍入数字。 与向上舍入过程类似,我们可以使用 math 或 decimal 模块。
使用 math.floor()
math 模块中的 floor() 函数的工作原理如下:它将数字向下舍入到小于该数字的最大整数。
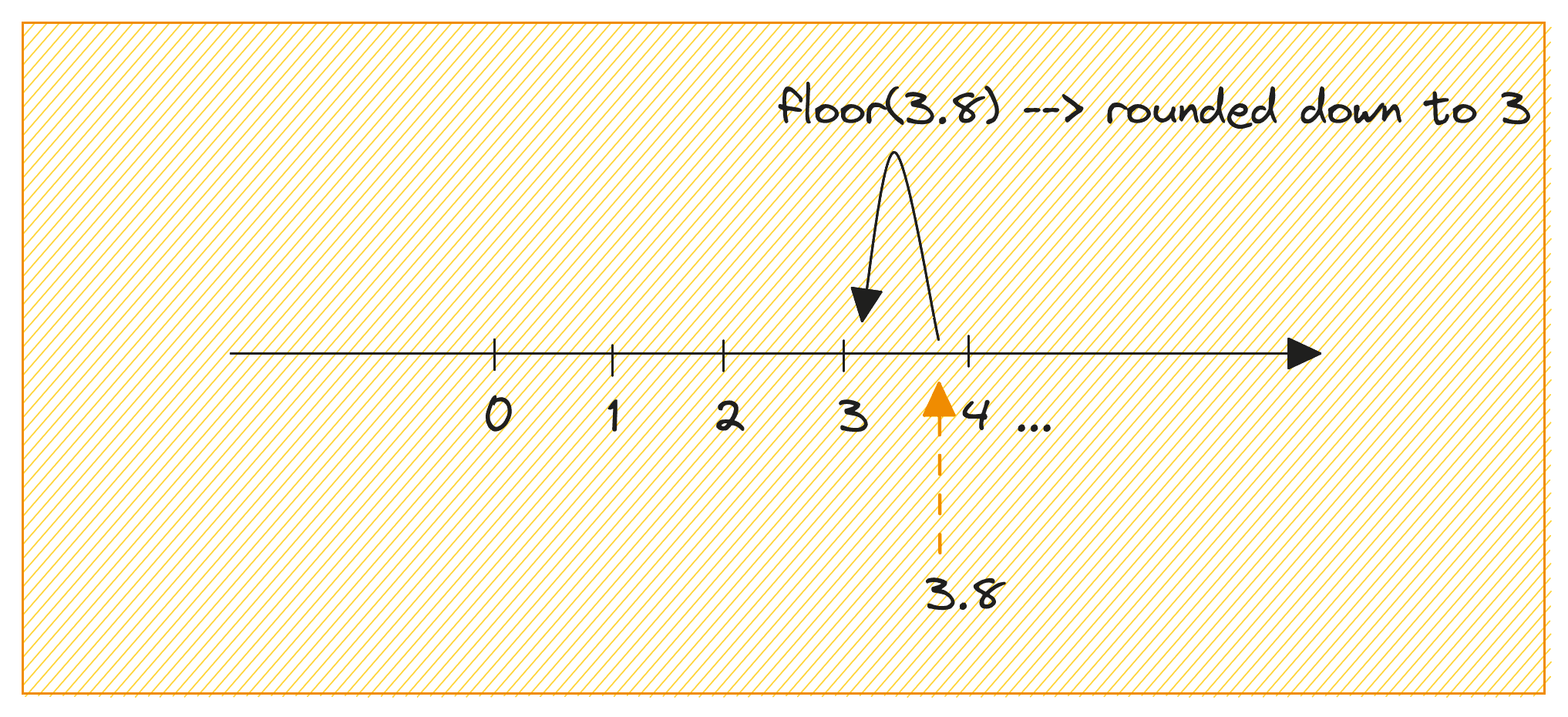
让我们看下面的例子:
import math number = 3.8 rounded_down = math.floor(number) print(rounded_down) # 输出:3
此处,floor() 函数将浮点数 3.8 向下舍入为 3。
使用 decimal 模块
要向下舍入数字,可以通过将舍入模式设置为 ROUND_FLOOR 来使用 quantize()。
from decimal import Decimal, ROUND_FLOOR
number = Decimal('3.8')
rounded_down = number.quantize(Decimal('0'), rounding=ROUND_FLOOR)
print(rounded_down)
# 输出:3
如图所示,3.8 已向下舍入为 3。
对数字进行舍入时要避免的常见陷阱
我们已经看到 round() 函数将一半舍入到偶数,这可能并不总是理想的。 在 Python 中舍入数字时,还需要避免一些其他常见陷阱:
- 不正确的相等比较:舍入数字通常会引入舍入误差。 如果你尝试在舍入结果与另一个值之间执行相等比较,则相等检查将(几乎总是)由于精度不同而失败。 因此,尽量避免浮点数和舍入后的浮点数之间的相等检查。 如果需要比较,则引入一个容差阈值。
- 信息丢失:你可能需要使用高精度捕获某些数据,例如不同时间戳的传感器读数。 将此类数据舍入到更少的小数位会导致信息丢失和不正确的分析。
- 对中间结果进行舍入:作为计算的一部分,通常会使用多个步骤。 在所有步骤中保持一致的精度。 此外,避免在中间步骤进行舍入,以防止舍入误差累积。
Python 中数字舍入的最佳实践
让我们列出在 Python 中对数字进行舍入时应遵循的一些最佳实践:
- 选择正确的数据类型:根据应用程序,在浮点数和小数数据类型之间做出选择。 如果需要高精度的浮点数运算,请选择
decimal数据类型。 - 使用一致的精度级别:在整个程序中为小数设置一致的精度级别,以避免意外的舍入错误。
- 记录舍入技术:在涉及货币和传感器读数等数据的实际应用中,采用一致且记录在案的舍入技术非常重要。
总结
让我们快速回顾一下我们学到的内容,以结束本教程:
- 你可以通过
round(num, ndigits)语法使用内置的round()函数。 使用round()函数时,应该了解银行家舍入策略。 因此,它将两个整数之间的数字精确舍入到最接近的偶数。 - 你可以使用
math模块中的ceil()和floor()函数,分别将给定数字向上舍入和向下舍入到最接近的整数。 - 当需要进行高精度的浮点数运算时,可以使用
decimal模块。 可以使用所需的精度和舍入策略对数字进行舍入。 - 你应了解 Python 中舍入数字的常见陷阱。 其中包括舍入造成的信息丢失、中间步骤的舍入结果,以及在代码的不同部分使用不同的精度。
- 最佳实践包括根据应用程序选择正确的数据类型,并记录一致的精度水平。
接下来,学习如何在Python中进行向下取整。
本文是否有帮助?
感谢您的反馈意见!