理解算法效率:大O分析详解
大O分析是一种用于评估和比较算法效率的强大工具。它帮助我们选择既高效又具有良好扩展性的算法。 本文将作为一份大O速查表,深入解析大O符号的相关知识。
什么是大O分析?
大O分析的核心在于考察算法在输入规模增大时效率的变化。 具体来说,我们关注的是,当算法处理的数据量增加时,其性能表现如何。
效率主要体现在系统资源的使用上,例如时间和内存。 在大O分析中,我们主要关注以下两个问题:
- 当输入规模增长时,算法的内存消耗如何变化?
- 当输入规模增长时,算法的运行时间如何变化?
第一个问题的答案被称为“空间复杂度”,而第二个问题则对应“时间复杂度”。 我们使用一种特殊的符号系统,即“大O符号”来表达这些复杂度,这将在后续部分详细介绍。
前置知识
为了更好地理解本文内容,您需要具备一定的代数基础。 此外,由于本文会提供Python代码示例,了解一些Python编程知识也会有所帮助。 但不必过于深入,因为您无需编写任何代码。
如何进行大O分析
本节将逐步介绍如何执行大O分析。
在进行大O复杂度分析时,务必记住算法的性能会受到输入数据结构的影响。
例如,对于排序算法而言,当列表中的数据已经按照正确顺序排列时,算法的执行速度最快,这被称为最佳情况。 相反,当数据以相反的顺序排列时,算法的执行速度最慢,被称为最坏情况。
在进行大O分析时,我们通常只考虑算法在最坏情况下的表现。
空间复杂度分析

我们首先来探讨如何进行空间复杂度分析。我们需要关注的是,随着输入规模的扩大,算法所使用的额外内存如何增长。
例如,下面这个函数使用递归方式从n循环到零。它的空间复杂度与n成正比。 这是因为当n增大时,调用堆栈上的函数调用数量也会相应增加, 因此其空间复杂度为O(n)。
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
以下是更高效的实现方式:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
在上述代码中,我们仅创建了一个额外的变量并用它来进行循环。 即使n变得非常大,我们也只会用到一个额外变量。 因此,此算法的空间复杂度是恒定的,表示为O(1)。
通过对比上述两个算法的空间复杂度,我们可以得出结论:使用while循环比递归更高效。 这正是大O分析的意义所在:评估算法在处理不同大小输入时的性能差异。
时间复杂度分析

进行时间复杂度分析时,我们并不关心算法执行的绝对时间,而是关注算法所执行的计算步骤随输入规模增长的趋势。 这是因为实际的运行时间会受到许多难以量化且随机的系统因素影响。 因此,我们只跟踪计算步骤的增长,并假定每个步骤的耗时相等。
为了更好地说明时间复杂度分析,请看下面的示例:
假设我们有一个用户列表,其中每个用户都包含ID和姓名信息。 现在我们需要实现一个函数,在给定用户ID时返回用户名。 一种实现方式如下:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
对于一个给定的用户列表,我们的算法会遍历整个用户数组,直到找到具有匹配ID的用户。 当列表中有3个用户时,算法会执行3次迭代; 当有10个用户时,则执行10次迭代。
可见,算法的执行步骤数与用户数量呈线性关系。 因此,该算法的时间复杂度是线性的。 但是,我们还可以优化此算法。
假设我们不是将用户存储在列表中,而是将其存储在字典中。 那么,我们查找用户的算法如下:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
使用新的算法,假设字典中有3个用户,我们需要执行固定数量的步骤来获取用户名。 如果用户数量增加到10个,我们仍然只需要执行相同数量的步骤。 随着用户数量的增长,获取用户名的步骤数量保持不变。
因此,这个新的算法具有恒定的时间复杂度。 无论有多少用户,执行的计算步骤数量都是相同的。
什么是大O符号?
在前文中,我们讨论了如何计算不同算法的大O空间复杂度和时间复杂度, 并用线性或常数等词汇来描述复杂度。 大O符号是另一种描述复杂度的常用方法。
大O符号是一种表示算法空间或时间复杂度的表示方式。 它以”O”后跟一个括号的形式呈现,括号内是一个关于输入规模n的函数,用来表示特定的复杂度。
线性复杂度用n来表示,所以我们将其写成O(n)(读作“O of n”)。 常数复杂度用1表示,所以写成O(1)。
还有其他更多类型的复杂度,我们将在下一节讨论。 总的来说,要计算算法的复杂度,可以遵循以下步骤:
- 尝试推导一个关于n的数学函数f(n),其中f(n)表示算法使用的空间量或计算步骤,n是输入规模。
- 选择该函数中增长速度最快的项。 各项的增长速度由快到慢依次为:阶乘、指数、多项式、二次、线性、对数、常数。
- 删除该项的所有系数。
最终的结果就是我们在括号中使用的表达式。
举个例子:
考虑以下Python函数:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
现在,我们来计算一下这个算法的大O时间复杂度。
首先,我们用一个数学函数f(n)来表示算法执行的计算步骤数。 回想一下,n代表输入规模。
从代码可以看出,该函数执行两个操作:一是计算用户数量,二是打印用户数量。 接着,对于每个用户,它执行两个操作:一是打印索引,二是打印用户。
因此,表示计算步骤数的函数可以写成f(n) = 2 + 2n。其中n代表用户数量。
接着第二步,我们选择增长最快的项。2n是一个线性项,2是一个常数项。线性项的增长速度比常数项快,因此我们选择2n,即线性项。
所以,我们的函数现在是f(n) = 2n。
最后一步是删除系数。在我们的函数中,系数是2,我们将其删除。函数就变成了f(n) = n。 这就是我们在括号中使用的项。
因此,此算法的时间复杂度是O(n),也就是线性复杂度。
不同的大O复杂度
接下来,我们将介绍不同的大O复杂度,并附上相应的图表。
#1. 常数复杂度

常数复杂度意味着算法使用的空间量(在分析空间复杂度时)或执行的步骤数(在分析时间复杂度时)是固定的。 这是一个理想的复杂度,因为随着输入的增长,算法不需要额外的资源或时间。 因此,它具有很强的可扩展性。
常数复杂度表示为O(1)。 但是,要设计出以常数复杂度运行的算法并非总是可能的。
#2. 对数复杂度
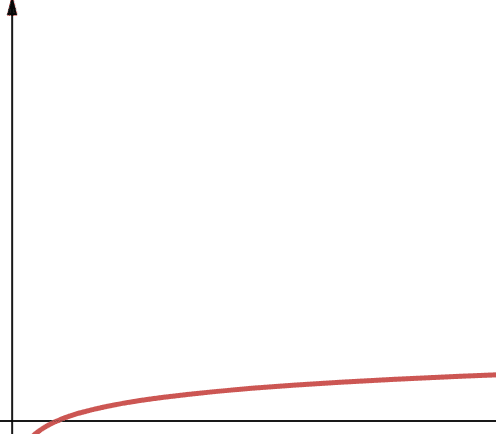
对数复杂度表示为O(log n)。 需要注意的是,在计算机科学中,如果没有指定对数的底数,则默认为2。
因此,log n 等同于log2n。 我们知道对数函数在开始时增长速度很快,然后逐渐放缓。 这意味着对数函数可以很好地处理不断增长的输入规模,具有较强的扩展性。
#3. 线性复杂度
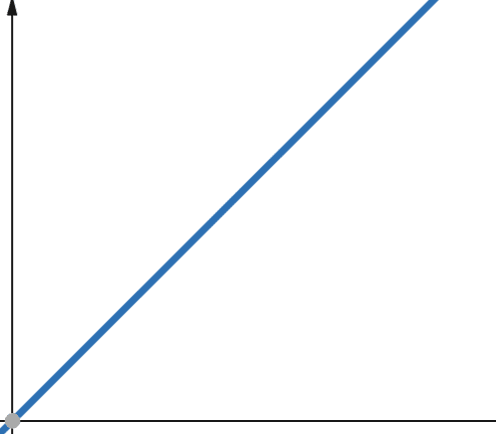
对于线性函数,如果自变量按比例因子p缩放,那么因变量也会按相同的因子p缩放。
因此,具有线性复杂度的函数会以与输入规模相同的比例增长。 如果输入规模增加一倍,那么计算步骤数或内存使用量也会增加一倍。 线性复杂度用符号O(n)表示。
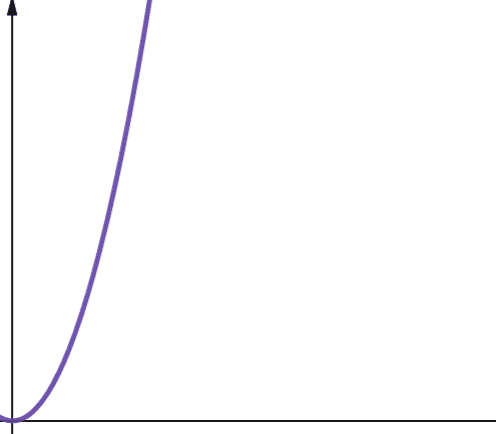
#4. 线性对数复杂度
O(n * log n)表示线性对数复杂度。 线性对数函数是线性函数乘以对数函数的结果。 当log n 大于 1 时,线性对数函数产生的结果略大于线性函数。这是因为当乘以大于1的数时,n会增大。
对于所有大于2的n值,Log n 都大于1 (请记住,log n 是log2n)。 因此,对于任何大于2的n值,线性对数函数的扩展性不如线性函数。 而大多数情况n都大于2。 因此,线性对数函数的扩展性通常比线性函数差。
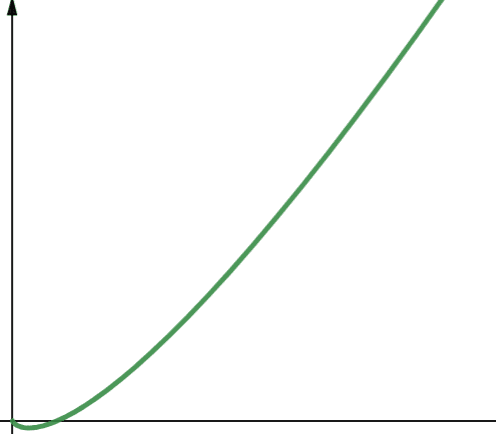
#5. 二次复杂度
二次复杂度表示为O(n^2)。 这意味着,如果输入规模增加10倍,则执行的步骤数或使用的空间会增加10^2倍,即100倍! 这意味着其扩展性较差,从图中也可以看到,复杂度会快速增长。
二次复杂度常出现在嵌套循环的算法中,例如冒泡排序,其中外层循环执行n次,内层循环也执行n次。 虽然二次复杂度通常不理想,但有时我们别无选择,只能采用具有二次复杂度的算法。
#6. 多项式复杂度
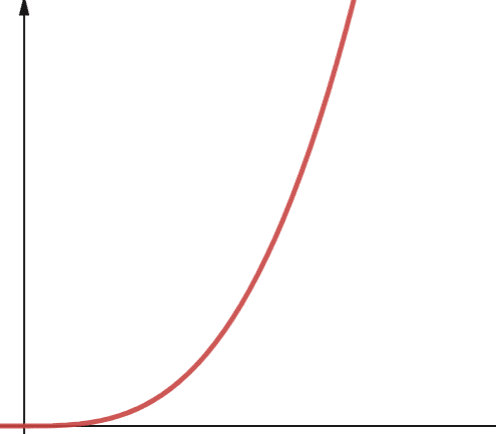
具有多项式复杂度的算法表示为O(n^p),其中p是某个常数整数。 p 表示n的幂次。
当存在大量的嵌套循环时,就会出现多项式复杂度。 多项式复杂度和二次复杂度之间的区别在于,二次复杂度的幂次是2,而多项式复杂度的幂次可以是任何大于2的数字。
#7. 指数复杂度
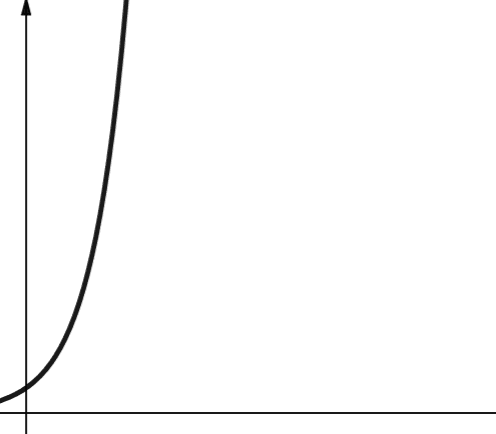
指数复杂度的增长速度比多项式复杂度还要快。 在数学中,指数函数的默认底数是常数e(欧拉数)。 然而,在计算机科学中,指数函数的默认底数是2。
指数复杂度用符号O(2^n)表示。 当n为0时,2^n为1。但是当n增加到5时,2^n就会增加到32。n增加1,就会使之前的结果翻倍。 因此,指数函数的扩展性非常差。
#8. 阶乘复杂度
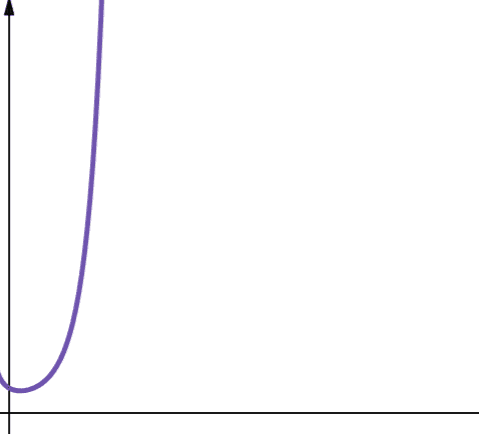
阶乘复杂度用符号O(n!)表示。 阶乘函数的增长速度也很快,因此扩展性较差。
总结
本文介绍了大O分析以及如何计算大O复杂度。 我们还讨论了各种不同的复杂度,并探讨了它们的扩展性。
接下来,您可以尝试使用大O分析来研究Python的排序算法。