本篇教程将引导你学习如何使用 Python 打印指定行数的帕斯卡三角形。
我们将从理解帕斯卡三角形的构造方式开始，然后编写 Python 函数，并探讨如何进一步优化该函数。
▶️ 让我们开始吧！
什么是帕斯卡三角形？如何构建它？
打印指定行数的帕斯卡三角形是一个常见的面试编程问题。
在一个拥有 n 行的帕斯卡三角形中，第 i 行包含 i 个元素。
第一行只有一个元素，其值为 1。后续行中的每个元素都是其正上方两个数字之和。
下图展示了如何构造一个五行的帕斯卡三角形。
numRows = 5 的帕斯卡三角形（作者创作）
注意，当某个数字上方只有一个数字时，我们是如何用零填充的。
📝 作为一个练习，尝试按照上述步骤构建 n = 6 和 n = 7 的帕斯卡三角形。
接下来，让我们开始编写代码。你可以直接在 techblik.com 的 Python IDE 上运行这些代码片段，以便在本教程中实践。
Python 函数实现帕斯卡三角形的打印
在这一节中，我们将编写一个 Python 函数来打印任意给定行数的帕斯卡三角形。
有两个关键问题需要考虑：
- 如何表示帕斯卡三角形中的每一个条目？
- 如何以适当的间距和格式打印帕斯卡三角形？
现在，让我们来解答这些问题。
#1. 如何表示帕斯卡三角形中的每个条目？
实际上，我们可以使用 nCr 公式来计算帕斯卡三角形中的条目。如果你还记得学校数学，nCr 表示从 n 个项目中选择 r 个项目的方法数。
nCr 的公式如下：
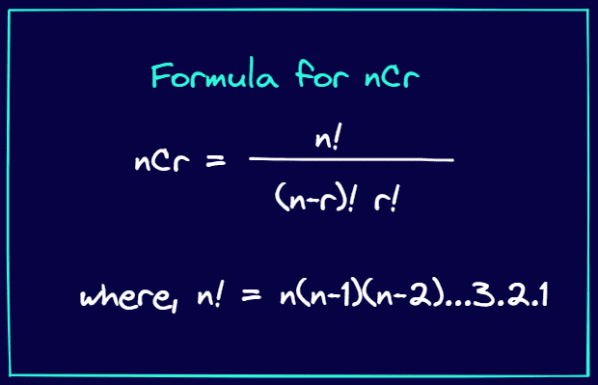nCr 公式（作者创作）
现在，让我们使用 nCr 公式来表达帕斯卡三角形中的条目。
使用 nCr 表示的帕斯卡三角形条目（作者创作）
我们现在找到了表示矩阵中条目的方法。
#2. 如何调整打印图案时的间距？
在一个具有 numRows 的帕斯卡三角形中，第 1 行有 1 个条目，第 2 行有 2 个条目，依此类推。为了将图案打印成三角形，你需要在第 i 行添加 numRows – i 个空格。你可以使用 Python 的 range 函数和 for 循环来实现这一点。
由于 range 函数默认不包括端点，请确保添加 + 1 以获得所需的前导空格数。
现在你已经了解了如何表示条目以及如何调整间距来打印帕斯卡三角形，让我们开始定义函数 pascal_tri。
函数定义解析
你希望函数 pascal_tri 实现什么功能？
- 函数 pascal_tri 应该接受行数 (numRows) 作为参数。
- 它应该打印 numRows 行的帕斯卡三角形。
为了计算阶乘，我们将使用 Python 内置的 math 模块中的阶乘函数。
▶️ 运行以下代码单元以导入阶乘并在当前模块中使用它。
from math import factorial
以下代码段包含了函数定义。
def pascal_tri(numRows):
'''Print Pascal's triangle with numRows.'''
for i in range(numRows):
# 循环获取前导空格
for j in range(numRows-i+1):
print(end=" ")
# 循环获取第 i 行的元素
for j in range(i+1):
# nCr = n!/((n-r)!*r!)
print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")
# 在新行中打印每一行
print("\n")
函数的工作原理如下：
- 函数 pascal_tri 有一个必需的参数 numRows：行数。
- 总共有 numRows 行。对于每一行 i，我们在该行的第一个条目之前添加 numRows – i 个前导空格。
- 然后我们使用 nCr 公式来计算各个条目。对于第 i 行，条目是 iCj，其中 j = {0,1,2,..,i}。
- 注意我们使用 // 来执行整数除法，因为我们希望条目是整数。
- 在计算完一行中的所有条目后，在新行中打印下一行。
🔗 因为我们添加了一个 文档字符串，你可以使用 Python 的内置 help 函数或 __doc__ 属性来访问该函数的文档字符串。下面的代码片段展示了如何做到这一点。
help(pascal_tri) # 输出 #Help on function pascal_tri in module __main__: #pascal_tri(numRows) # Print Pascal's triangle with numRows. pascal_tri.__doc__ # 输出 #Print Pascal's triangle with numRows.
现在让我们继续调用该函数，并传入行数作为参数。
pascal_tri(3) # 输出 # 1 # 1 1 # 1 2 1
正如预期的那样，它输出了帕斯卡三角形的前 3 行。
使用递归打印帕斯卡三角形
在上一节中，我们确定了帕斯卡三角形中每个条目的数学表达式。但是，我们没有利用相邻两行中条目之间的关系。
实际上，我们可以使用上一行来计算下一行的条目。我们可以不使用这种方法，并提出函数 pascal_tri 的递归实现吗？
是的，让我们来实现一下！
在递归实现中，函数重复调用自身，直到满足基本情况。在帕斯卡三角形的构造中，我们从一个包含一个条目 1 的第一行开始，然后构建后续行。
因此，对 pascal_tri(numRows) 的函数调用会依次调用 pascal_tri(numRows-1) 等等，直到达到基本情况 pascal_tri(1)。
考虑打印帕斯卡三角形前 3 行的示例。下图说明了如何将递归调用压入堆栈，以及递归函数调用如何返回帕斯卡三角形的行。
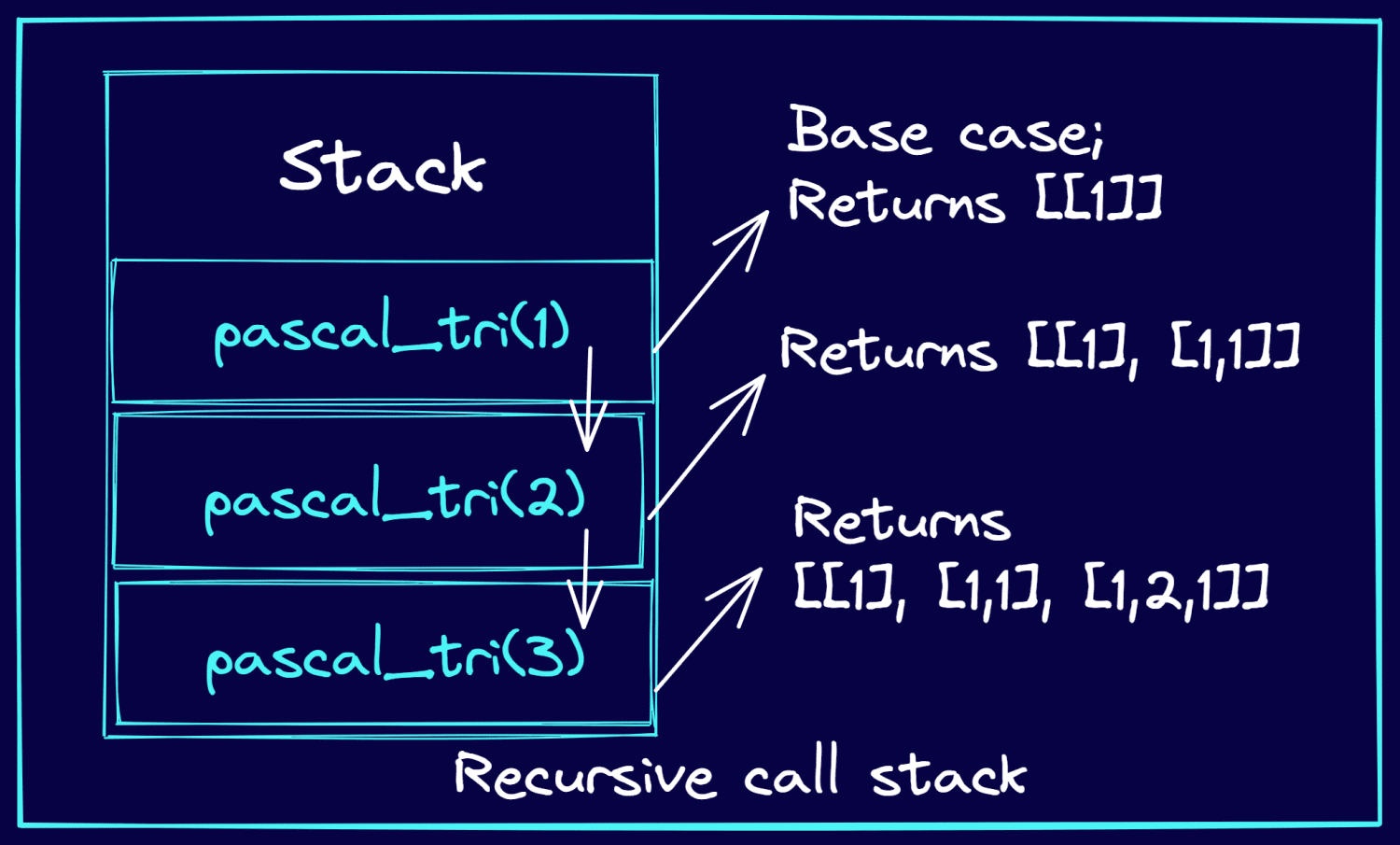递归调用期间的调用堆栈（作者创作）
▶️ 运行以下代码段，以递归方式生成帕斯卡三角形的行。
def pascal_tri(numRows):
'''Print Pascal's triangle with numRows.'''
if numRows == 1:
return [[1]] # 已达到基本情况！
else:
res_arr = pascal_tri(numRows-1) # 递归调用 pascal_tri
# 使用上一行计算当前行
cur_row = [1] # 每一行都以 1 开始
prev_row = res_arr[-1]
for i in range(len(prev_row)-1):
# 正上方两个条目的和
cur_row.append(prev_row[i] + prev_row[i+1])
cur_row += [1] # 每一行都以 1 结束
res_arr.append(cur_row)
return res_arr
这里有几个需要注意的点：
- 我们使用嵌套列表作为数据结构，其中帕斯卡三角形中的每一行本身就是一个列表，形式如下：[[row 1], [row 2],…,[row n]]。
- 函数调用 pascal_tri(numRows) 触发一系列递归调用，其中 numRows – 1, numRows – 2, 一直到 1 作为参数。这些调用被压入堆栈。
- 当 numRows == 1 时，我们达到了基本情况，函数返回 [[1]]。
- 现在，调用堆栈中的后续函数使用返回的列表来计算下一行。
- 如果 cur_row 是当前行，则 cur_row[i] = prev_row[i] + prev_row[i+1]— 当前索引正上方的 2 个元素的和。
由于返回的数组是一个嵌套列表（列表的列表），我们需要调整间距并打印条目，如下面的代码单元格所示。
tri_array = pascal_tri(5)
for i,row in enumerate(tri_array):
for j in range(len(tri_array) - i + 1):
print(end=" ") # 前导空格
for j in row:
print(j, end=" ") # 打印条目
print("\n") # 打印新行
输出结果如下，符合预期！
# 输出 # 1 # # 1 1 # # 1 2 1 # # 1 3 3 1 # # 1 4 6 4 1
打印 numRows ≤ 5 的帕斯卡三角形的 Python 函数
你学习的两种方法都可以打印任意行数 numRows 的帕斯卡三角形。
但是，有时你只需要打印较少行数的帕斯卡三角形。当你需要打印的行数最多为 5 行时，你可以使用一种简单的技巧。
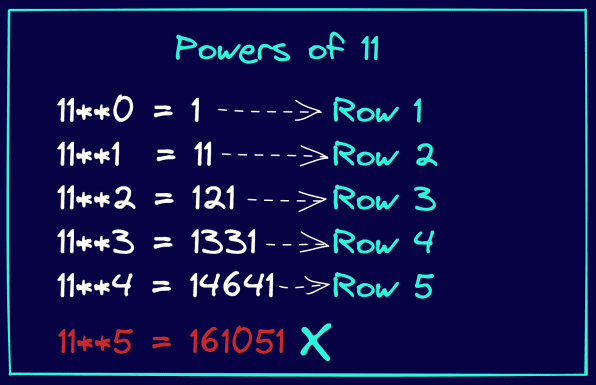
看看下图，并观察 11 的幂是如何与帕斯卡三角形中的条目相同的。另请注意，这仅适用于 11 的 4 次方。也就是说，11 的 {0,1,2,3,4} 次方给出了帕斯卡三角形第 1 行到第 5 行中的条目。
我们重写函数定义，如下所示：
def pascal_tri(numRows):
'''Print Pascal's triangle with numRows.'''
for i in range(numRows):
print(' '*(numRows-i), end='')
# 计算 11 的幂
print(' '.join(str(11**i)))
以下是函数 pascal_tri 的工作原理：
- 和前面的例子一样，我们调整了间距。
- 然后，我们使用 Python 的幂运算符 (**) 来计算 11 的幂。
- 由于 11 的幂默认是整数，我们使用 str() 将它们转换为字符串。你现在拥有了 11 的字符串形式的幂。
- Python 中的字符串是可迭代的——因此你可以循环遍历它们并一次访问一个字符。
- 接下来，你可以使用 join() 方法，语法如下：<sep>.join(<iterable>) ，它使用 <sep> 作为分隔符来连接 <iterable> 中的元素。
- 在这里，字符之间需要一个空格，所以 <sep> 将会是 ‘ ‘，<iterable> 是字符串：11 的幂。
让我们检查一下该函数是否按预期工作。
pascal_tri(5) # 输出 # 1 # 1 1 # 1 2 1 # 1 3 3 1 # 1 4 6 4 1
作为另一个示例，调用函数 pascal_tri 并以 4 作为参数。
pascal_tri(4) # 输出 # 1 # 1 1 # 1 2 1 # 1 3 3 1
我希望你现在知道如何轻松地打印 numRows 在 1 到 5 范围内的帕斯卡三角形。
结论
这是我们所学的：
- 如何构造具有给定行数的帕斯卡三角形。每行中的每个数字都是其正上方两个数字之和。
- 使用公式 nCr = n!/(nr)!.r! 编写 Python 函数计算帕斯卡三角形的条目。
- 然后，你学习了该函数的递归实现。
- 最后，你学习了构建 numRows 最大为 5 的帕斯卡三角形的最佳方法 – 使用 11 的幂。
如果你想提高 Python 技能，可以学习矩阵乘法，检查数字是否为素数，并解决字符串操作问题。祝你编程愉快！